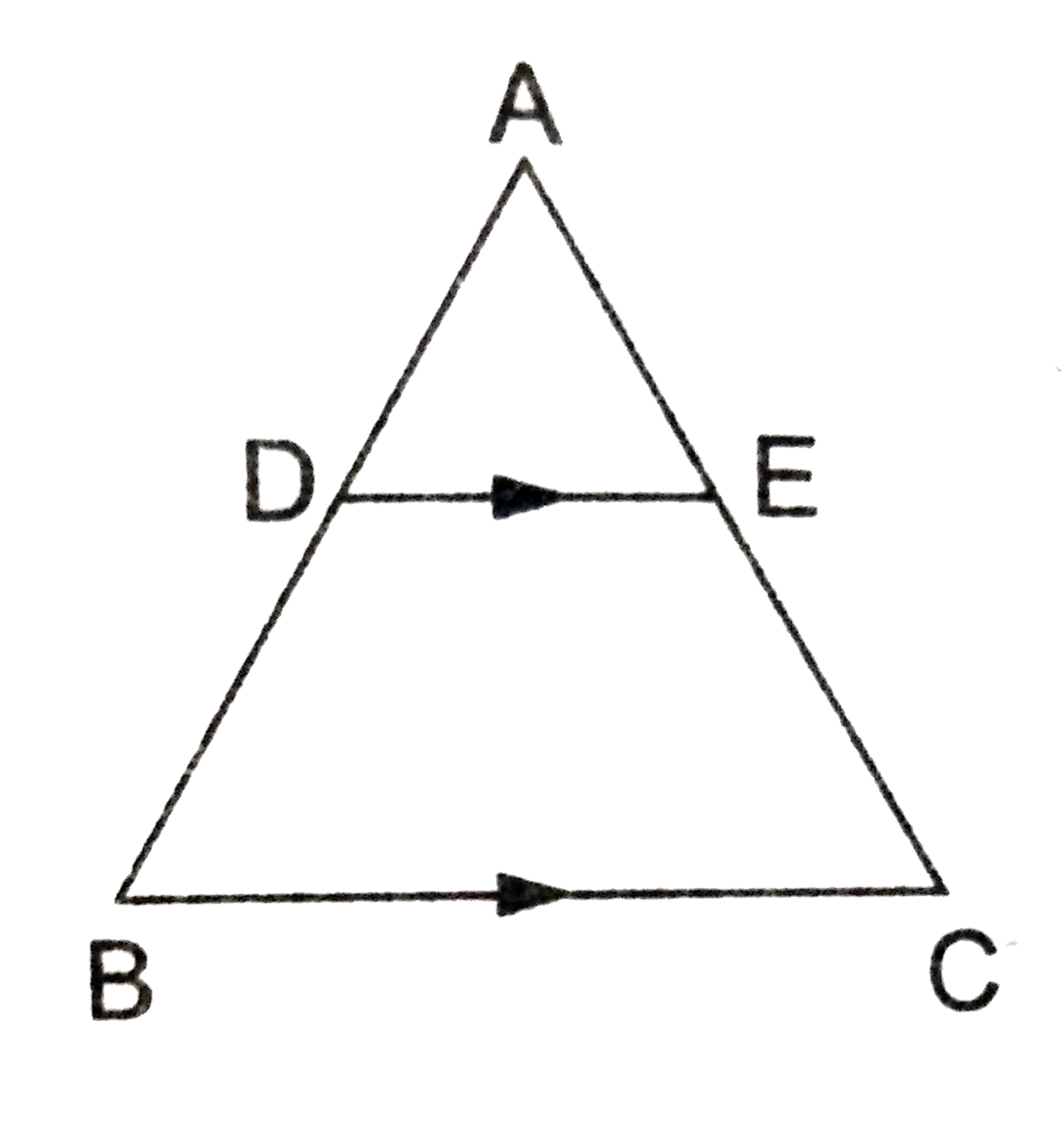
In ΔABC,DE∣∣BCsuch that ADBD=35. If AC=5.6cm, then AE is equal to
4.2 cm.
3.1 cm.
2.8 cm.
2.1 cm.
The correct Answer is:D
To solve the problem step by step, we will use the properties of similar triangles and the given ratio.
1. Understand the Given Information:
- We have triangle ABC.
- Line DE is parallel to BC.
- The ratio ADBD=35.
- The length AC=5.6cm.
2. Set Up the Ratios:
- Since DE is parallel to BC, by the Basic Proportionality Theorem (or Thales' theorem), we have:
ADBD=AEEC
- Given ADBD=35, we can set:
AD=3xandBD=5x
- Therefore, the total length of AB is:
AB=AD+BD=3x+5x=8x
3. Calculate the Lengths:
- Since AC is given as 5.6cm, we can express AC in terms of AE and EC:
AC=AE+EC
- From the ratio AEEC=ADBD=35, we can set:
AE=3yandEC=5y
- Therefore, the total length of AC becomes:
AC=AE+EC=3y+5y=8y
4. Relate the Two Expressions for AC:
- Since both expressions represent AC:
8y=5.6
- To find y:
y=5.68=0.7
5. Calculate AE:
- Now substituting y back to find AE:
AE=3y=3×0.7=2.1cm
Final Answer:
Thus, the length of AE is 2.1cm.
---
- We have triangle ABC.
- Line DE is parallel to BC.
- The ratio ADBD=35.
- The length AC=5.6cm.
- Since DE is parallel to BC, by the Basic Proportionality Theorem (or Thales' theorem), we have:
ADBD=AEEC
- Given ADBD=35, we can set:
AD=3xandBD=5x
- Therefore, the total length of AB is:
AB=AD+BD=3x+5x=8x
- Since AC is given as 5.6cm, we can express AC in terms of AE and EC:
AC=AE+EC
- From the ratio AEEC=ADBD=35, we can set:
AE=3yandEC=5y
- Therefore, the total length of AC becomes:
AC=AE+EC=3y+5y=8y
- Since both expressions represent AC:
8y=5.6
- To find y:
y=5.68=0.7
- Now substituting y back to find AE:
AE=3y=3×0.7=2.1cm
Thus, the length of AE is 2.1cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)30videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-II)25videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
Knowledge Check
- Question 1 - Select One
DE is a tangent to the circumcircle of ΔABC at the vertex A such that DE∣∣BC. If AB=17cm, then the length of AC is equal to
A16.0cmB16.8cmC17.3cmD17cm - Question 2 - Select One
In figure, DE∣∣BC and BD = 7.2 cm , CE = 5.4 cm and AE = 1.8 cm. Then AD is equal to :
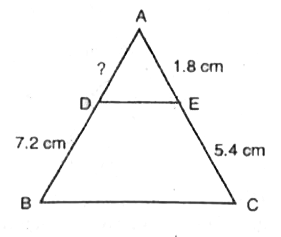 A4.2 cmB3.5 cmC2.4 cmDNone of these
A4.2 cmB3.5 cmC2.4 cmDNone of these - Question 3 - Select One
If in △ABC, D and E are the points on sides AC and BC, respectively such that DE || AB. F is the point on CE such that DF ||AE. If CE= 6cm and CF = 2.5 cm, then BC is equal to:
त्रिभुज ABC में, D और E क्रमशः भुजाओं AC तथा BC के मध्य बिंदु हैं जो इस प्रकार ह कि DE || AB है F, CE पर स्थित ऐसा बिंदु है कि DF|| AE है | यदि CE= 6 सेमी और CF =2.5 सेमी है, तो BC किसके बराबर है ?A12 cmB15.6 cmC14 cmD14.4 cm
In figure-2, DE∣∣BC. If ADDB=32 and AE=2.7 cm then EC is equal to
View SolutionIn a ΔABC, if DE is parallel to BC, ADDB=34 and AC = 15 cm, then find the length AE.
View SolutionIn ΔABC AD is angle bisector such that BD : DC = 2 : 3. If AB = 7 cm then find AC : BC.
View SolutionIn ΔABC , AD ⊥ BC such that AD2=BD×CD . Then ΔABC is a _________ at A .
 View Solution
View SolutionIn ΔABC,∠B=90∘andBD⊥AC.IfAC=9cmandAD=3 cm then BD is equal to
View Solution