The young's modulus of steel is twice that of brass . Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof .If we want the lower ends of the wires to be at the same level, then the weigths added to the steel and brass wires must be in the ratio of :Solution in Tamil
1:1
1:2
2:1
4:1
Step by step video & image solution for The young's modulus of steel is twice that of brass . Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof .If we want the lower ends of the wires to be at the same level, then the weigths added to the steel and brass wires must be in the ratio of : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two satellites of earth, S1 andS2 aremoving inthe same orbit.The mass of S1 is four times the mass of S2. Which oneofthe following statements s true?
View SolutionAssuming the sun to have a spherical outer surface of radiating like a black body at temperature t∘C, the power received by a unit surface,(normal to the incident rays) at a distance R from the centre of the sun is
View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View Solutionस्टील का यंग प्रत्यास्थता गुणांक, पीतल से दोगुना है | एक ही लम्बाई तथा एक ही अनुप्रस्थ काट के दो तारों, एक स्टील का तथा एक पीतल का, को एक ही छत से लटकाया जाता है | यदि, भार लटकाने पर, दोनों तारों के निचले सिरे एक ही तल पर हैं तो स्टील तथा पीतल के तारों से लटकाये भारों का अनुपात होना चाहिये :
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionThe Young's modulii of brass ans steel are in the ratio of 1:2. A brass wire and a steel wire of the same length are extended by the same amount under the same deforming force. If rB and rS are the radii of brass and steel wires respectively, then
View SolutionIf the ratio of lengths, radii and Young's modulus of steel and brass wires shown in the figure are a, b and c respectively, the ratio between the increase in lengths of brass and steel wires would be Brass and steel wire would be
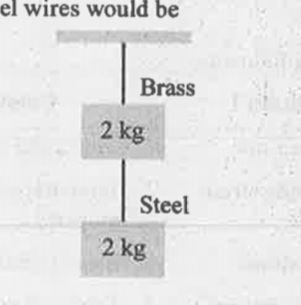
View SolutionThe Young's Modulus of steel is twice that of brass. Two wires of same length and of same area of cross-section, one of steel and another of brass are suspended from the same roof. If then the weights added to the steel and brass wires must be in the ratio of
View SolutionThe ratios of length areas of cross-section and Young's modulii of steel of that of brass wires shown in the figure are a,b and c respectively . The ratio of increase in the lengths of brass of that of steel wires is [Assume that the masses of steel and brass wires are negligible]
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of:
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View SolutionThe Young's modulus of steel is twice that of brass. Two wires of the same length and of the same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weight added to the steel and brass wires must be in the ratio of
View SolutionTwo Young's modulus of steel! is twice that of brass. Two wires of same length and of same area of cross section, one of steel and another of brass are suspended from the same roof. If we want the lower ends of the wires to be at the same level, then the weights added to the steel and brass wires must be in the ratio of :
View SolutionYoung modulus of steel is twice that of brass. These are two wires of steel and brass, of equal length and diameter of cross section, hung from the same roof. What is the ratio of the weights hanging at the ends of these two wires so that their bottom ends are at the same level (i.e. at the same height)?
View Solution
