The position of the centre of mass of a uniform semi-circular wire of radius 'R' placed in x-y plane with its centre at the origin and the line joining itsends as x-axis is given by (0,xRπ). Then the value of |x| is ______.
To find the value of |x| for the center of mass of a uniform semi-circular wire of radius 'R', we can follow these steps:
1. Understanding the Setup:
The semi-circular wire is placed in the x-y plane with its center at the origin (0,0). The ends of the wire are located at points (-R, 0) and (R, 0), forming a semi-circle above the x-axis.
2. Formula for Center of Mass:
The center of mass (CM) for a uniform semi-circular wire can be derived using symmetry and integration. The x-coordinate of the center of mass for a semi-circular wire is known to be 0 due to symmetry. The y-coordinate can be calculated using the formula:
ycm=1L∫ydl
where L is the length of the wire and dl is an infinitesimal length element.
3. Length of the Semi-Circular Wire:
The length L of the semi-circular wire is given by:
L=12×2πR=πR
4. Finding the y-coordinate of the Center of Mass:
The y-coordinate can be calculated as follows:
ycm=1πR∫π0Rsin(θ)⋅Rdθ
Here, Rsin(θ) gives the y-coordinate of the wire at angle θ, and Rdθ is the arc length element.
5. Evaluating the Integral:
The integral simplifies to:
ycm=R2πR∫π0sin(θ)dθ=Rπ(−cos(θ))π0=Rπ((−cos(π)+cos(0)))=Rπ(1+1)=2Rπ
6. Comparing with Given Coordinates:
The position of the center of mass is given as (0,xRπ). From our calculation, we found that:
ycm=2Rπ
Therefore, we can equate:
xRπ=2Rπ
7. Solving for x:
By simplifying the equation, we can cancel R (assuming R≠0):
x=2
8. Finding the Absolute Value:
Since we need the absolute value:
|x|=2
Final Answer:
The value of |x| is 2.
The semi-circular wire is placed in the x-y plane with its center at the origin (0,0). The ends of the wire are located at points (-R, 0) and (R, 0), forming a semi-circle above the x-axis.
The center of mass (CM) for a uniform semi-circular wire can be derived using symmetry and integration. The x-coordinate of the center of mass for a semi-circular wire is known to be 0 due to symmetry. The y-coordinate can be calculated using the formula:
ycm=1L∫ydl
where L is the length of the wire and dl is an infinitesimal length element.
The length L of the semi-circular wire is given by:
L=12×2πR=πR
The y-coordinate can be calculated as follows:
ycm=1πR∫π0Rsin(θ)⋅Rdθ
Here, Rsin(θ) gives the y-coordinate of the wire at angle θ, and Rdθ is the arc length element.
The integral simplifies to:
ycm=R2πR∫π0sin(θ)dθ=Rπ(−cos(θ))π0=Rπ((−cos(π)+cos(0)))=Rπ(1+1)=2Rπ
The position of the center of mass is given as (0,xRπ). From our calculation, we found that:
ycm=2Rπ
Therefore, we can equate:
xRπ=2Rπ
By simplifying the equation, we can cancel R (assuming R≠0):
x=2
Since we need the absolute value:
|x|=2
The value of |x| is 2.
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - A)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - PHYSICS (SECTION - B)
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
The moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionThe moment of inertia of a uniform semicircular wire of mass M and radius R about an axis passing through its centre of mass and perpendicular to its plane is xMR210. Find the value of x? (Take π2=10)
View Solution
Knowledge Check
A ring with a uniform charge Q and radius R, is placed in the yz plane with its centre at the origin
Athe field at the origin is zeroBThe potential at the origin is kQRCthe potential at the origin is kQx2Dthe filled at the point (x,0,0) is kQR2+x2An electric dipole is placed along x-axis with its centre at origin:
AThe electric field is perpendicular to each and every point on y−z planeBy−z plane is an equipotential surfaceCy−z plane is not equipotential surfaceDFlux of electrix field enclosing dipole is zeroA current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with x>0 is now bent so that it now lies in the y-z plane.
AThe magnitude of magnetic moment now diminishesBThe magnetic moment does not changeCThe magnitude of →B at (0,0,z),z>>R increasesDThe magnitude of →B at (0,0,z),z>>R is unchanged
Find coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionFind the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R

View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
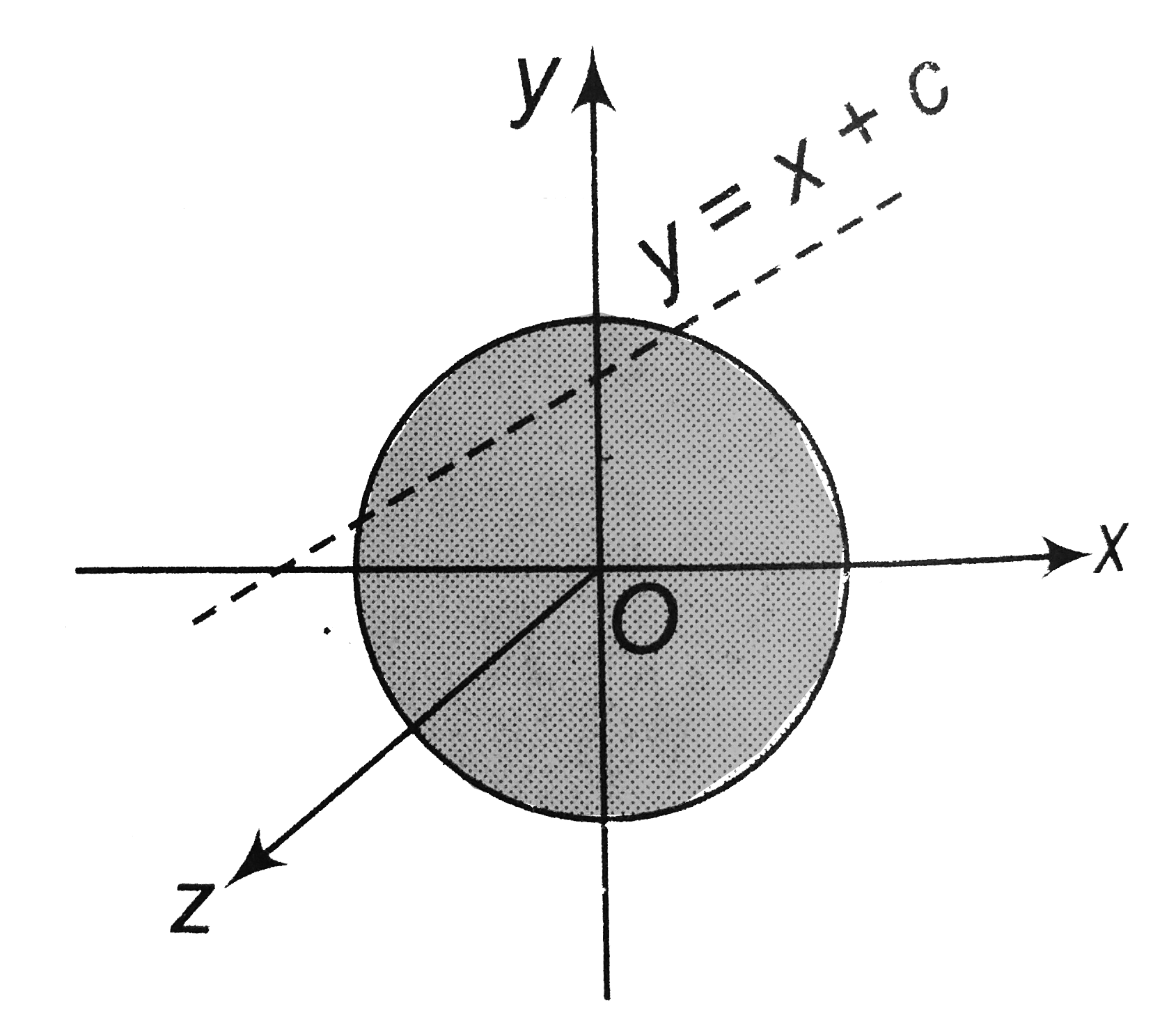 .
.
View SolutionA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionThe moment of inertia of a uniform semicircularwire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is :
View Solution
