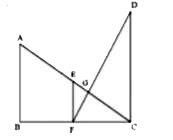
AB, EF and CD are parallel lines. Given that EG = 5 cm, GC = 10 cm, AB = 15 cm and DC = 18 cm, find AC?
20 cm
24 cm
25 cm
28 cm
The correct Answer is:C
Step by step video, text & image solution for AB, EF and CD are parallel lines. Given that EG = 5 cm, GC = 10 cm, AB = 15 cm and DC = 18 cm, find AC? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- CENTRE OF TRIANGLEBOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B
8 Videos
- ALGEBRAIC IDENTITIES BOOK - LUCENT PUBLICATIONCHAPTER - ALGEBRAIC IDENTITIES EXERCISE - Exercise - 1B
28 Videos
- CIRCLE AND ITS TANGENT LINESBOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8B
27 Videos
Similar Questions
In a trapezium ABCD, AB and DC are parallel sides and ∠ADC=90∘ . If AB = 15 cm, CD = 40 cm and diagonal AC = 41 cm. Then the area of the trape- zium ABCD is:
View SolutionIn a circle, AB and DC are two chords. When AB and DC are produced, they meet at P. If PC = 5.6 cm, PB = 6.3 cm and AB = 7.7 cm, then the length of CD is:
View Solution
Knowledge Check
AB, EF and CD are parallel lines. Given that EG=5cm, GC= 10 cm, AB = 15 cm and DC= 18 cm. What is the value of AC?
A20 cmB24 cmC25 cmD28 cm-
AB, EF and CD are parallel lines. Given that EG = 5 cm, GC = 10 cm, AB = 15 cm and DC = 18 cm, find AC?A21 cmB25 cC18 cmD28 cm In figure, AB, EF and CD are parallel lines. Given that GE = 5 cm, GC = 10 cm and CD = 18 cm, then EF is equal to
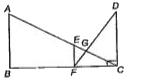A11 cmB5 cmC6cmD9cm
ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
View SolutionIn the given figure, if AB = 10 cm, CD = 7 cm, SD = 4 cm and AS = 5 cm, then BC = ?
View SolutionABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
View SolutionIn ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
View SolutionChords AB and CD of a circle intersect at a point P inside the circle. If AB = 10 cm, AP = 4 cm and PC = 5 cm, then CD is equal to:
View Solution