Two ions of masses 4 amu and 16 amu have charges +2e and +3e respectively. These ions pass through the region of constant perpendicular magnetic field. The kinetic energy of both ions is same. Then :
lighter ion will be deflected more than heavier ion
no ion will be deflecled
lighter ion will be deflected less than heavier ion
both ions will be deflected equally
To solve the problem, we need to analyze the motion of two ions with different masses and charges in a magnetic field, given that they have the same kinetic energy.
1. Understanding the Motion in a Magnetic Field:
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path (r) can be expressed as:
r=mvqB
where:
- m is the mass of the ion,
- v is the velocity of the ion,
- q is the charge of the ion,
- B is the magnetic field strength.
2. Relating Velocity to Kinetic Energy:
The kinetic energy (KE) of the ions is given by:
KE=12mv2
From this, we can express the velocity v in terms of kinetic energy:
v=√2⋅KEm
3. Substituting Velocity into the Radius Formula:
Substitute v into the radius formula:
r=m√2⋅KEmqB=√2⋅KE⋅mqB
This shows that the radius depends on the mass, charge, and kinetic energy.
4. Calculating the Radius for Each Ion:
For the first ion (mass = 4 amu, charge = +2e):
r1=√2⋅KE⋅42eB=√8⋅KE2eB
For the second ion (mass = 16 amu, charge = +3e):
r2=√2⋅KE⋅163eB=√32⋅KE3eB
5. Comparing the Radii:
To compare r1 and r2:
r1=√8⋅KE2eBandr2=√32⋅KE3eB
We can factor out the common terms:
r1=k⋅√82andr2=k⋅√323
where k=√KEeB.
6. Numerical Comparison:
Now we need to compare √82 and √323:
- √82=2√22=√2
- √323=4√23
Since 4√23>√2, we conclude that:
r2>r1
7. Conclusion:
Since r1<r2, the first ion (4 amu, +2e) will have a smaller radius and thus will be deflected more than the second ion (16 amu, +3e).
Final Answer:
The lighter ion (4 amu, +2e) will be deflected more than the heavier ion (16 amu, +3e).
---
When a charged particle moves in a magnetic field, it experiences a magnetic force that causes it to move in a circular path. The radius of this circular path (r) can be expressed as:
r=mvqB
where:
- m is the mass of the ion,
- v is the velocity of the ion,
- q is the charge of the ion,
- B is the magnetic field strength.
The kinetic energy (KE) of the ions is given by:
KE=12mv2
From this, we can express the velocity v in terms of kinetic energy:
v=√2⋅KEm
Substitute v into the radius formula:
r=m√2⋅KEmqB=√2⋅KE⋅mqB
This shows that the radius depends on the mass, charge, and kinetic energy.
For the first ion (mass = 4 amu, charge = +2e):
r1=√2⋅KE⋅42eB=√8⋅KE2eB
For the second ion (mass = 16 amu, charge = +3e):
r2=√2⋅KE⋅163eB=√32⋅KE3eB
To compare r1 and r2:
r1=√8⋅KE2eBandr2=√32⋅KE3eB
We can factor out the common terms:
r1=k⋅√82andr2=k⋅√323
where k=√KEeB.
Now we need to compare √82 and √323:
- √82=2√22=√2
- √323=4√23
r2>r1
Since r1<r2, the first ion (4 amu, +2e) will have a smaller radius and thus will be deflected more than the second ion (16 amu, +3e).
The lighter ion (4 amu, +2e) will be deflected more than the heavier ion (16 amu, +3e).
Topper's Solved these Questions
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B)
40 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section A )
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics Section B
20 Videos
- JEE MAINS 2020BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2020EXERCISE - PHYSICS
246 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
Similar Questions
Does a charge Particle gain K.E. when passed through magnetic field region? Justify.
View SolutionTwo particles of masses m and 2m having same charges q each are placed in a uniform electric field E and allowed to move for the same time.If the ratio of their kinetic energies is ab then the value of a+b is _(--)
View Solution
Knowledge Check
Mixed He+ and O2+ ions (mass of He+=4 amu and that of O2+=16 amu) beam passes a region of constant perpendicular magnetic field. If kinetic energy of all the ions is same then
AHe+ ions will be deflected more than those of O2+BHe+ ions will be be deflected less than those of O2+CAll the ions will be deflected equallyDNo ions will be deflectedTwo bodies of masses 3 m and 6 m have some momentum Their respective kinetic encics E1 and E2 are in the ratia
A1:2B2:1C√2:1D1:1Two bodies of masses m and 2m have same momentum. Their respective kinetic energies E1 and E2 are in the ratio
A1:2B2:1C1:√2D1:4
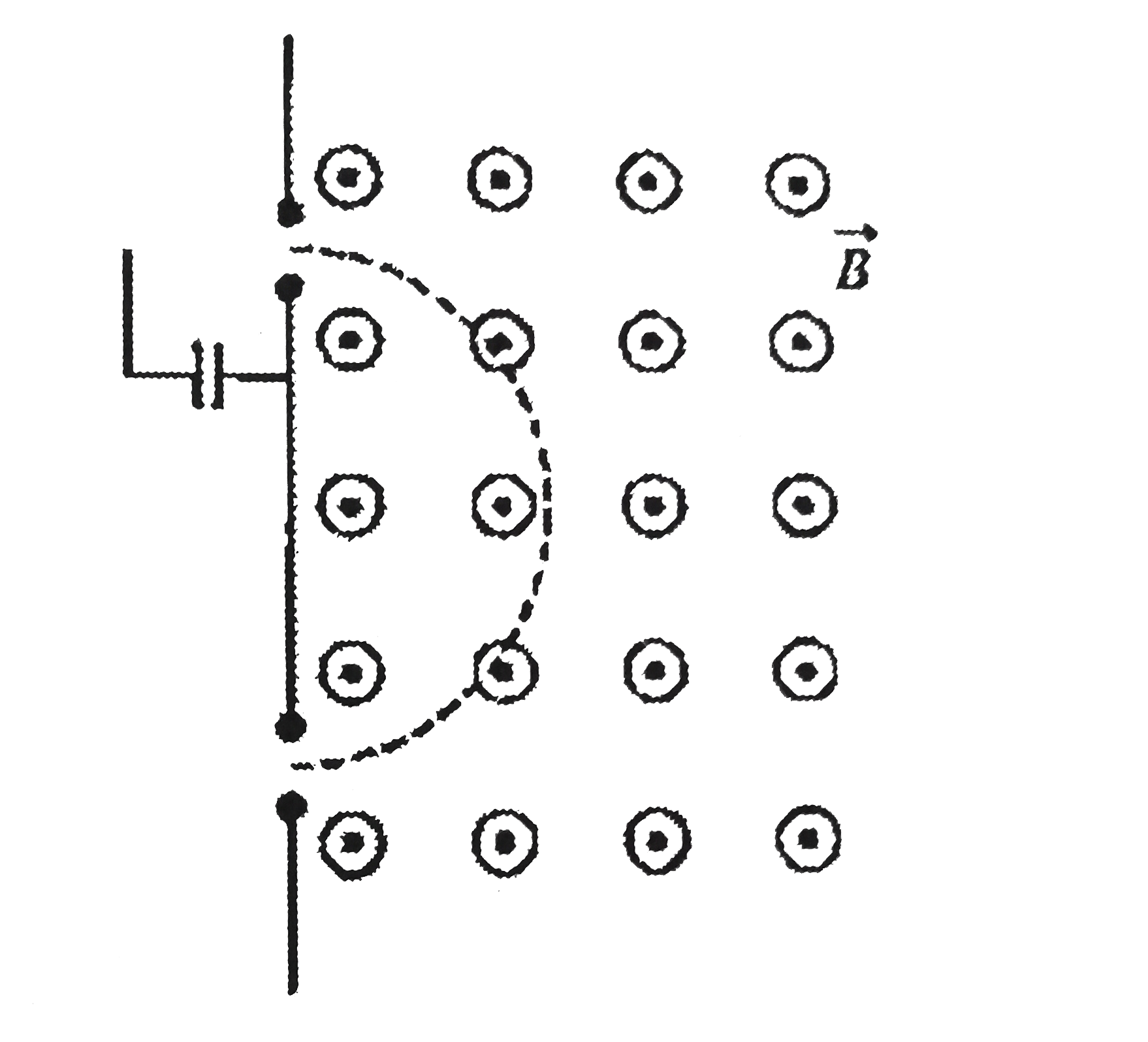
A mass spectrometer is a device which selelct particle of equal mass. An ion with an electric charge q>0. Starts at rest from s ource S and is accelerated through a potential difference V. it passes thorugh a hole into a region of constant magnetic field →B perpendicular to the plane of the paper as shown in the figure-4.233. The particle is deflected by the magnetic field and emerges thorugh the bottom hole at a distance d from the top hole. The mass of the particle is:
View SolutionA charged particle of charge q and mass m enters perpendiculalry in a magnetic field B. Kinetic energy of particle E, then frequency of rotation is
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionTwo charged particles of charge +2q and +q have masses m and 2m respectively. Then are kept in uniform electric field allowed to move for the same time. Find the ratio of their kinetic energies.
View SolutionTwo particles of mass m and 2m with charges 2q and q are placed in a uniform electric field E and allowed to move for same time. Find the ratio of their kinetic energie
View Solution
