A coaxial line carries the same current i up the inside conductor of radius a as down the outer conductor of inner radius b and outer radius c. The magnetic induction field at distance r from the conductor.
The magnetic field at a distance r from the conductor when b<r<c is
μ0i2πr[1−(r2−b2)(c2−b2)]
μ0i2πr[1+(r2−b2)(c2−b2)]
μ0i2πr2[1−(r2−b2)(c2−b2)]
μ0i2πr2[1−(c2−r2)(r2−b2)]
The correct Answer is:A
When b<r<c, Here current enclosed by co-axial circular path of radius r.
Current passing through inner conductor-current pasing through portions of outer conductor lying between r = b and r = c (-ve sign is used because the currents in two conductors are in opposite direction)
Br Ampere.s law B2πr=μ0[i−iπ(c2−b2)×π(r2−b2)]
∴B=μ0i2πr[1−(r2−b2)(c2−b2)]
Similar Questions
A coaxial cable carries the a current i in the inside conductor of radius a as shown in figure-4.80 and the outer conductor of inner radius b and outer radius c carries a current i' in opposite direction. Find the magnetic induction due to the coaxial cable at distance r from the central axis of the cable for (a) r>a, (b) a<r<b and (c) b>r>c

View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View Solution
Knowledge Check
A current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
A∞BZeroCμ04π2irDμ04π2πrrVariation of magnetic field with distance from current carrying conductor is:
AB∝a2BB∝1a2CB∝aDB∝1aA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
A B
B C
C D
D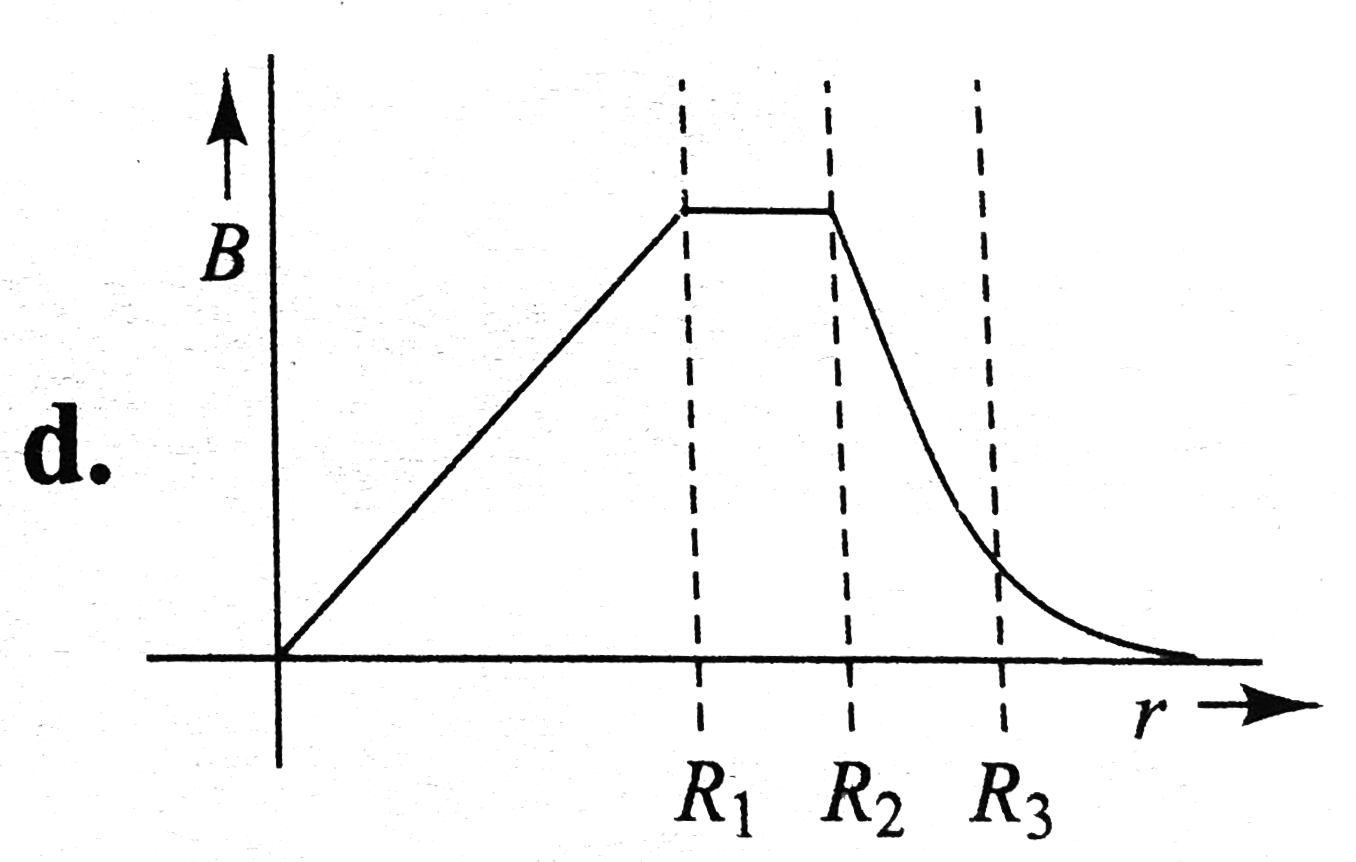
A coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View SolutionCharge Q is given to a spherical conductor of radius R. It is surrounded by a concentric conducting shell of inner radius a and outer radius b. Corresponding electric field diagram will be:
View SolutionIf the current density in a linear conductor of radius 'a' varies with r according to relation J=kr2, where k is a constant and r is the distance of a point from the axis of conductor. Find the magnetic field induction at a point distance r from the axis, when (i) r<a and (ii) r>a.
View Solution
