A particle of mass m and charge q is released from rest in a uniform field of magnitude E. The uniform field is created between two parallel plates of charge densities +σand−σ, respectively. The particle accelerates toward the other plate a distance d apart. Determine the speed at which it strikes the opposite plate.
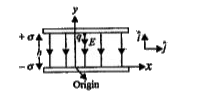
The applied electric field is →E=−E0ˆj. The force experienced by the charge q is
→F=q→E=−qE0ˆj
The force is constant, and so the acceleration is constant as well, i.e.,
¯a=¯¯¯Fm=−qE0mˆj............(a)
Because of constant acceleration, the particle moves in the negative y-direction, the problem is analogous to the motion of a mass released from rest in a gravitational field. From equations of motion, we get
vy=vy0+ayt=0+−qE0mt...........(b)
and y=y0+v0t+12ayt2or0=d+0−12qE0mt2..........(c)
The particle starts at y0=d, and impact occurs at y=0.
From Eq. (c ), we get
vy=−qE0m(2dmqE0)1/2=−√2qE0dm
Similar Questions
A particle of mass ma and charge q is released from rest in a uniform filed of magnitude E. the uniform field is created between two parallel plates of charge densities +σ and −σ, respectively. The particle accelerates toward the other plate a distance d apart. Determine the speed at which it stirkes the opposite plate.

View SolutionA particle of mass ma and charge q is released from rest in a uniform filed of magnitude E. the uniform field is created between two parallel plates of charge densities +σ and −σ, respectively. The particle accelerates toward the other plate a distance d apart. Determine the speed at which it stirkes the opposite plate.

View Solution
Knowledge Check
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2tA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2tA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
A B
B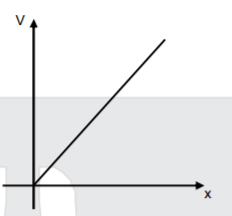 C
C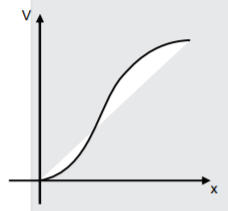 D
D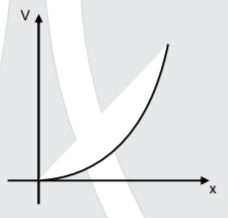
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionA charge of mass .m. charge .2e. is released from rest in a uniform electric field of strength .E.. The time taken by it to travel a distance .d. in the field is
View Solution
