ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24cm2, then ar (ABC) = 24cm2.Solution in Punjabi
Step by step video & image solution for ABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24 cm^2, then ar (ABC) = 24 cm^2. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
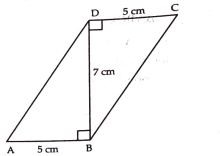 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)
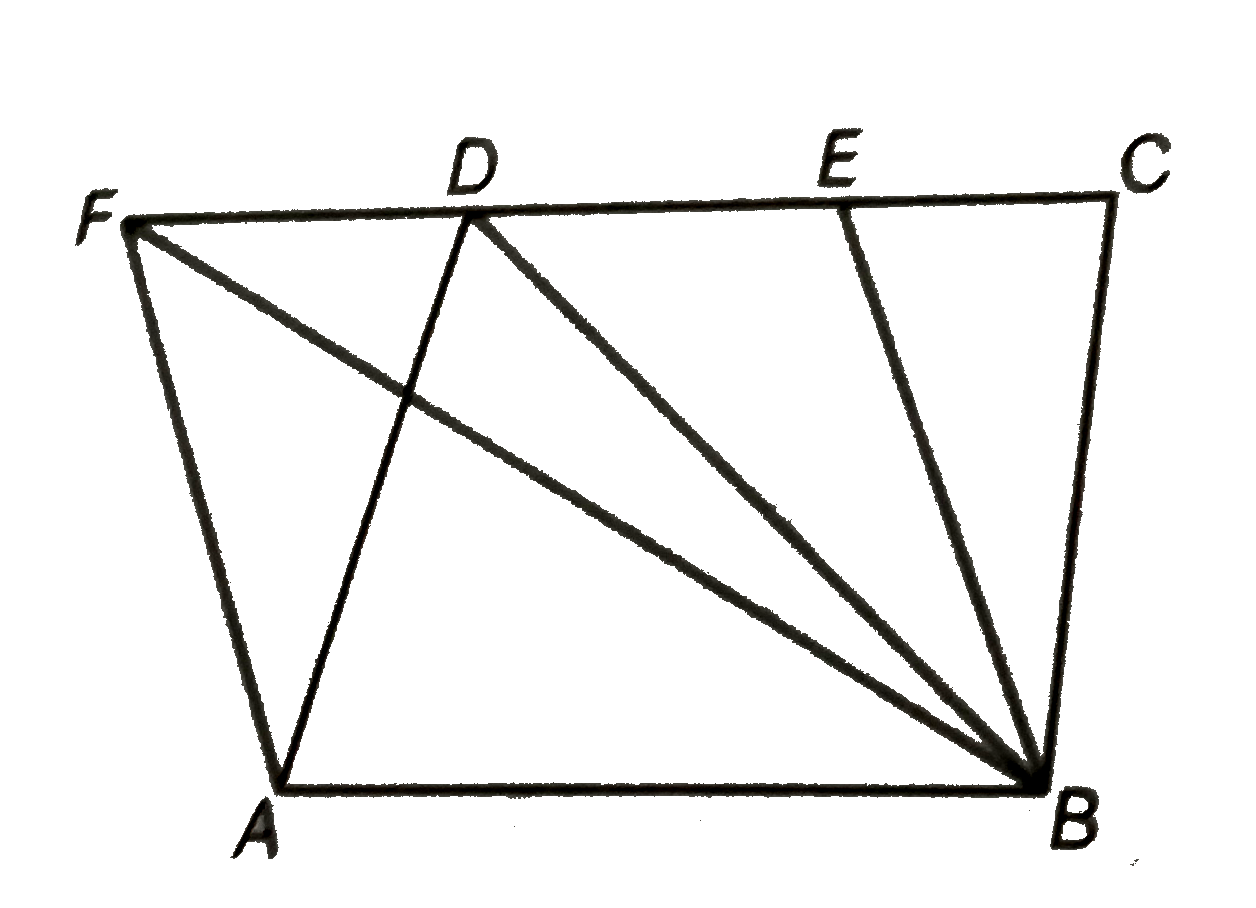
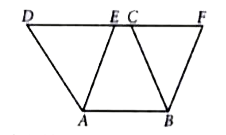
View SolutionIn the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
View SolutionABCD एक समान्तर चतुर्भुज और X भुजा AB का मध्य-बिंदु है । यदि ar(AXCD)=24cm2 है, तो ar(ABC)=24cm2 है।
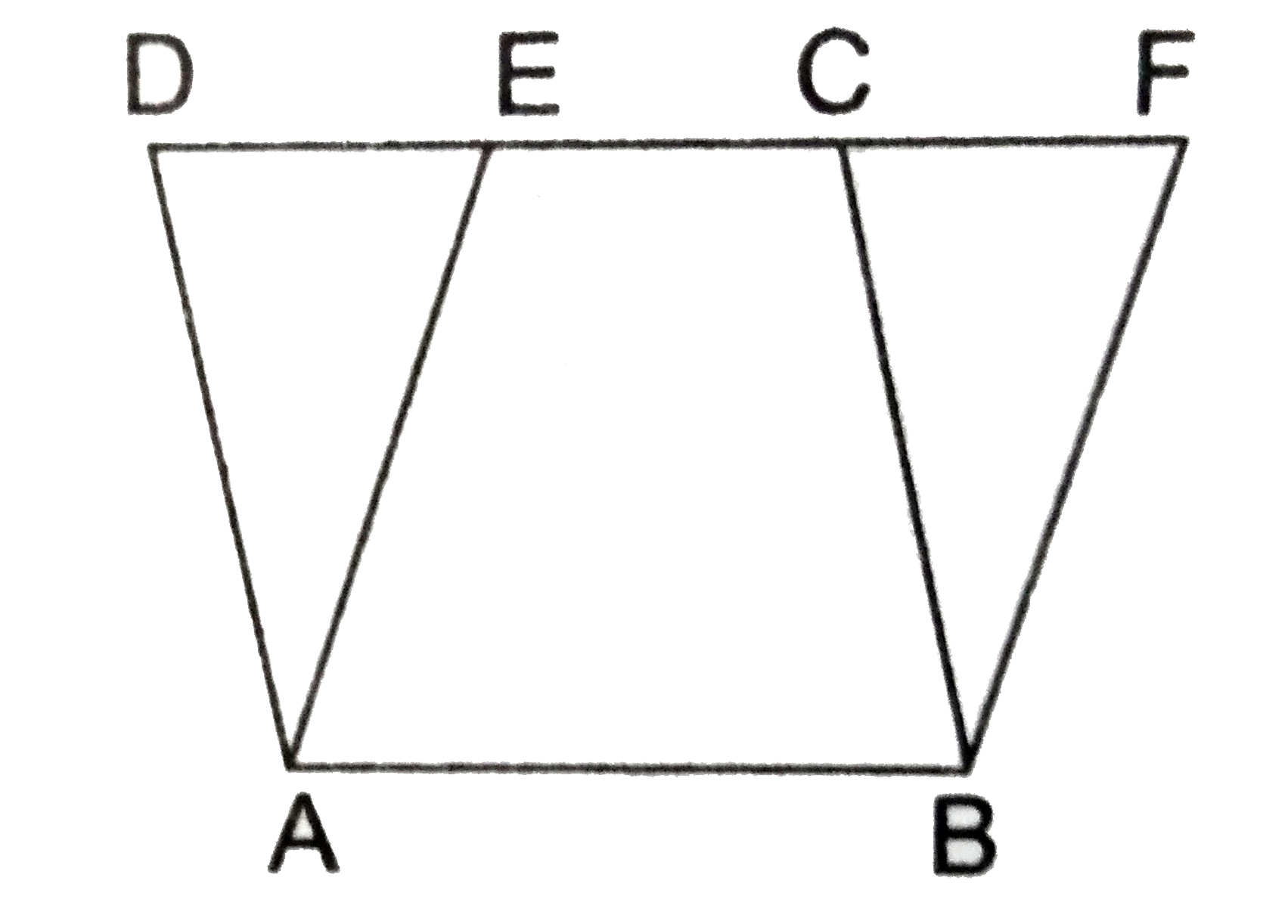
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
View SolutionABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
View SolutionThe area of the parallelogram ABCD is 90CM2. Find
(i) ar (ABEF) (ii) ar (ΔABD)
(iii) ar (ΔBEF)

View SolutionABCD is a square . If ar(ABCD)=36 cm2 . Then AB=____ cm.
View SolutionFor parallelogram ABCD, ar(ABCD)=48 cm2 . Then ar(ABC)=___ cm2
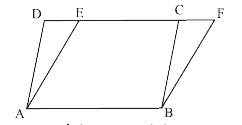
View SolutionIn figure, ABCD and EFGD are two parallelograms and G is the mid-point of side CD. Then, ar (DPC) = (1)/(2) ar(EFGD).
View SolutionIn the given fig.
 ABCD is a parallelogram and ABE is a triangle. Also AB∣∣CE. If ar (ABCD) = 60cm2 then ar (ΔABE) is :
ABCD is a parallelogram and ABE is a triangle. Also AB∣∣CE. If ar (ABCD) = 60cm2 then ar (ΔABE) is :
View SolutionABCD is a parallelogram and X is the mid-point of AB. If ar (AXCD) = 24cm2, then ar (ABC) = 24cm2.
View SolutionABCD is a parallelogram. If ar (ABC) = 18 cm2, then are (ABCD) = …………….. cm2
View SolutionIn the given figure, ABCD and ABFE are parallelograms such that ar(quad. EABC) =19 cm2 and ar(||gm ABCD) = 28 cm2. Then, ar(△BCF) is
View Solution
