ΔABC~ΔDEF such that DE = 3 cm , EF = 2 cm , DF = 2.5 and BC = 4 cm . Find the perimeter of ΔABC.
To find the perimeter of triangle ABC given that triangle ABC is similar to triangle DEF, we can follow these steps:
Step 1: Write the ratios of the sides
Since the triangles are similar, the ratios of their corresponding sides are equal. We can express this as:
ABDE=BCEF=ACDF
Step 2: Substitute the known values
From the problem, we know:
- DE=3cm
- EF=2cm
- DF=2.5cm
- BC=4cm
Substituting these values into the ratios, we have:
AB3=42=AC2.5
Step 3: Simplify the ratios
Calculating 42:
42=2
So, we can rewrite the ratios as:
AB3=2andAC2.5=2
Step 4: Solve for AB and AC
1. To find AB:
AB=3×2=6cm
2. To find AC:
AC=2.5×2=5cm
Step 5: Calculate the perimeter of triangle ABC
The perimeter P of triangle ABC is given by the sum of its sides:
P=AB+BC+AC
Substituting the values we found:
P=6+4+5=15cm
Final Answer
The perimeter of triangle ABC is 15cm.
---
Since the triangles are similar, the ratios of their corresponding sides are equal. We can express this as:
ABDE=BCEF=ACDF
From the problem, we know:
- DE=3cm
- EF=2cm
- DF=2.5cm
- BC=4cm
AB3=42=AC2.5
Calculating 42:
42=2
So, we can rewrite the ratios as:
AB3=2andAC2.5=2
1. To find AB:
AB=3×2=6cm
AC=2.5×2=5cm
The perimeter P of triangle ABC is given by the sum of its sides:
P=AB+BC+AC
Substituting the values we found:
P=6+4+5=15cm
The perimeter of triangle ABC is 15cm.
Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )
11 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
8 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Multiple Choice Questions)
5 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Knowledge Check
If ΔABC~ΔDEF such that 2AB=DEandBC=6cm find EF.
A6 cmB12 cmC10 cmD8 cmΔABC is such that AB = 3 cm, BC = 2 cm, CA = 2.5 cm. If ΔABC~ΔDEF and EF= 4 cm, then perimeter of ΔDEF is :
A7.5 cmB15 cmC22.5 cmD30 cmIf ΔABC is similar to ΔDEF such that BC = 3 cm, EF = 4 cm and area of ΔABC=54cm2, then the area of ΔDEF is :
A66cm2B78cm2C96cm2D54cm2
Find the perimeter of ΔABC, if AP=12 cm

View SolutionIf ΔABC~ΔDEF AB =4 cm , DE = 6 cm, EF =9 cm and FD =12 cm find the perimeter of ΔABC .
View SolutionR and s are points on the sides DE and EF respectively of a ΔDEF such that ER = 5 cm , RD = 2.5 cm , SE = 1.5 cm and FS = 3.5 cm .Find whether RS||DF or not .
View SolutionIf ΔABC is similar to ΔDEF such that BC=3cm,EF=4cm and area of ΔABC=54cm2. Find the area of ΔDEF.
View SolutionIn Figure , find the perimeter of ΔABC. If AP = 12 cm.
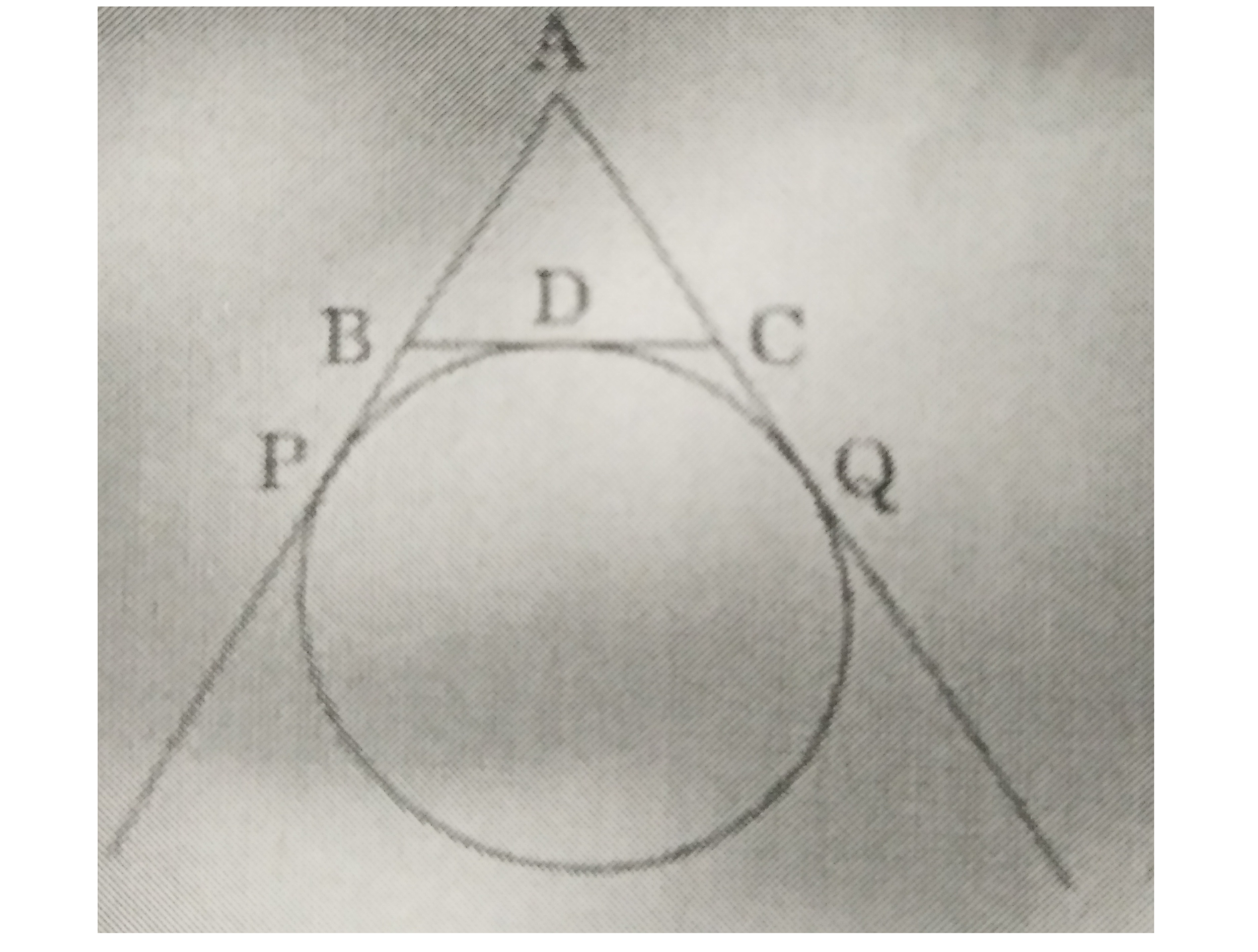
View Solution
