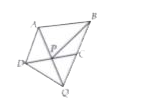
In the figure ,ABCD is a parallelogram and E divides BC in the ratio 1:3 DB and AE intersect at F. Show that DF = 4FB and AF = 4FE .
Step by step video & image solution for In the figure ,ABCD is a parallelogram and E divides BC in the ratio 1:3 DB and AE intersect at F. Show that DF = 4FB and AF = 4FE . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )
11 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Multiple Choice Questions)
8 Videos
- DIKSHA QUESTIONS BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Multiple Choice Questions)
5 Videos
- COORDINATE GEOMETRYBOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT
20 Videos
- INTRODUCTION TO TRIGONOMETRY BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment
15 Videos
Similar Questions
Knowledge Check
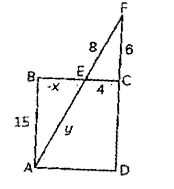
In the given figure, Here, ABCD is a parallellogram in which DC is extended to F such that AF intersects BC at E.
Perimeter of ΔABE=A35cmB36cmC40cmD45cmABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
Point Q divides DB in the ratioA1:2B1:3C3:1D2:1ABCD is a parallelogram. L is a point on BC which divides BC in the ratio 1:2. AL intersects BD at P.M is a point on DC which divides DC in the ratio 1:2 and AM intersects BD in Q.
PQ:DB is equal toA2/3B1/3C1/2D3/4
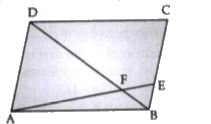
ABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
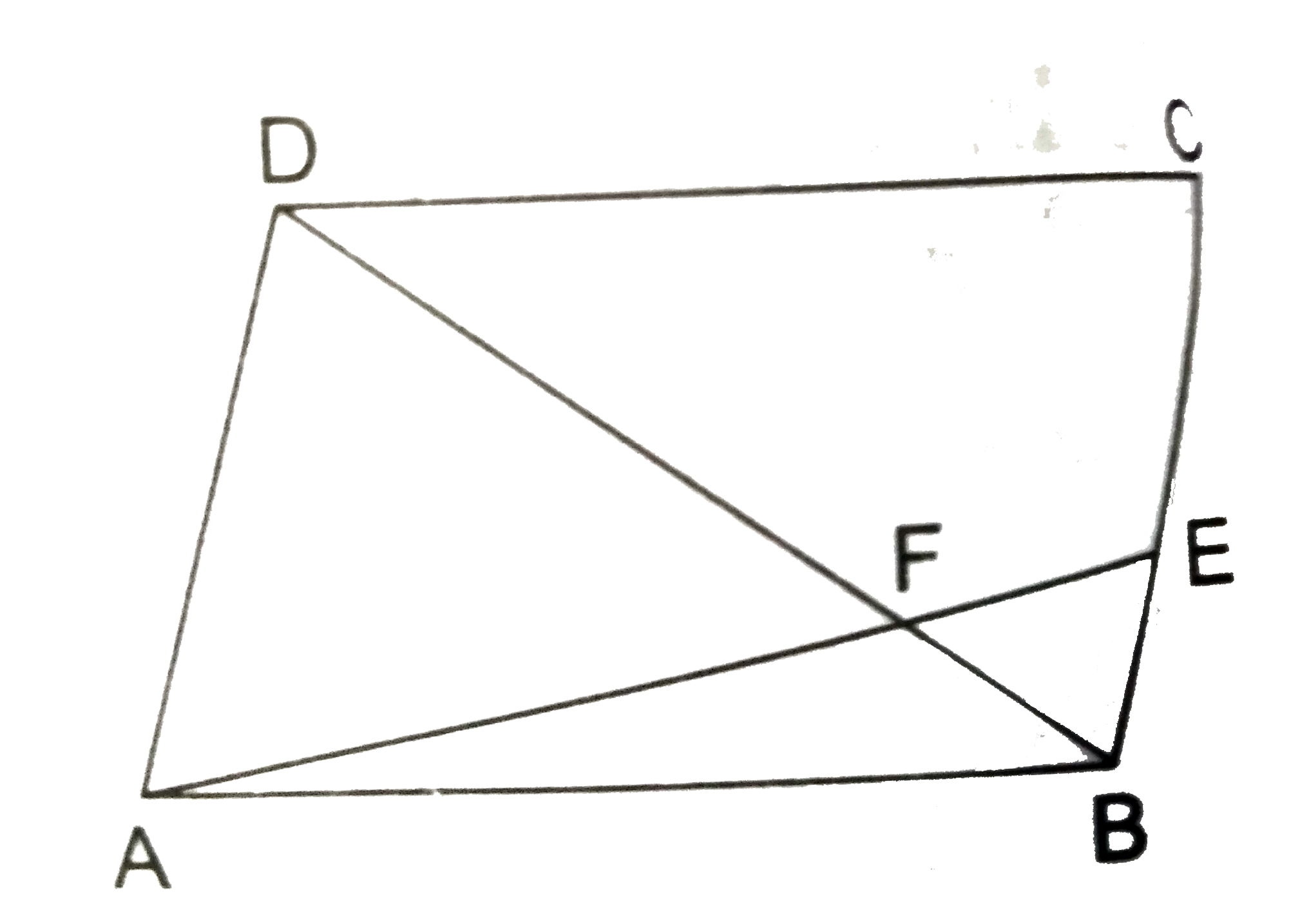
View SolutionIn the given figure, ABCD is a parallelogram. AE divides the line segment BD in the ratio 1 : 2. If BE = 1.5 cm find BC.

View SolutionIn the given figure, ABCD is a parallelogram and E is the midpoint of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.

View SolutionThe side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
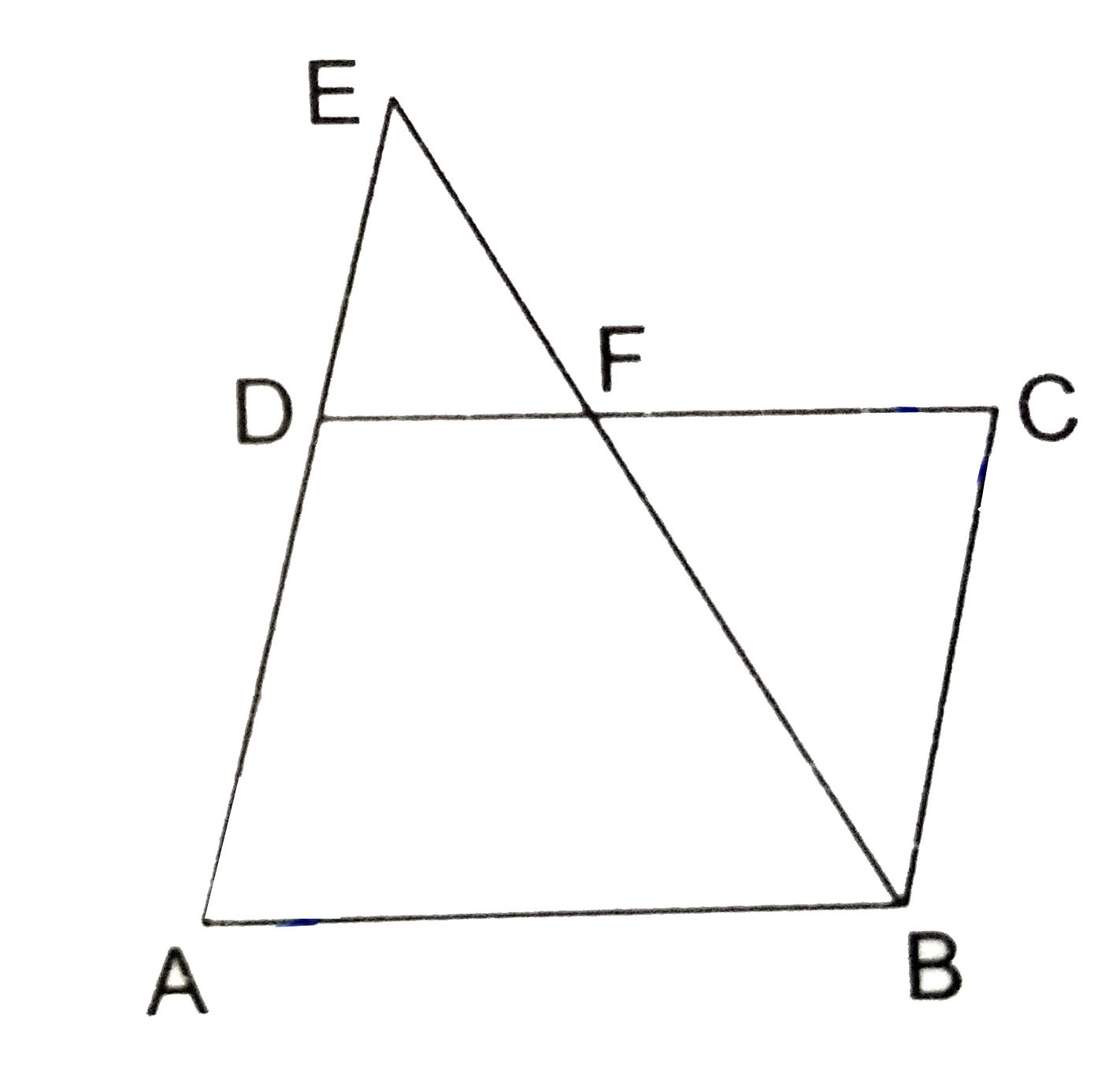
View SolutionIn the given figure, ABCD is a parallelogram in which DC is extended to F such that AF intersects BC at E . Then perimeter of ΔABE=
View Solution