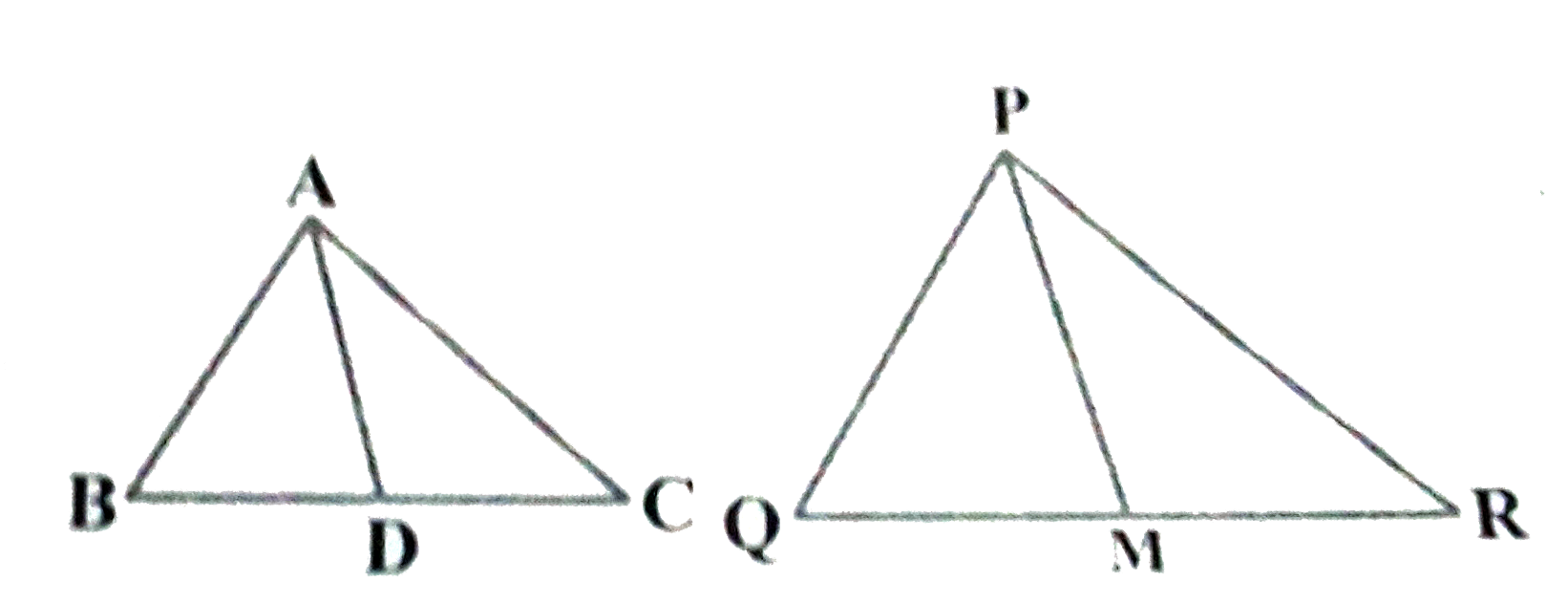
If AD and PM are medians of triangles ABC and PQR, respectively where, prove that
Step by step video solution for If AD and PM are medians of triangles ABC and PQR, respectively whereDeltaA B C DeltaP Q R, prove that (A B)/(P Q)=(A D)/(P M) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 2019BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2019EXERCISE - Section - D
12 Videos
- SAMPLE PAPER 2019BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2019EXERCISE - Section - B
8 Videos
- SAMPLE PAPER 2 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - D
9 Videos
- SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 3 [CBSE 2019 (TOPPER SOLVED)]EXERCISE - SECTION - D
12 Videos
Similar Questions
If AD and PM are medians of triangles ABC and PQR, respectively whereΔABC~ΔPQR, prove that ABPQ=ADPM
View SolutionAD and PM are medians of triangles ABC and PQR respectively where ΔABC~ΔPQR. Prove that: ABPQ=ADPM.
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP

View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ

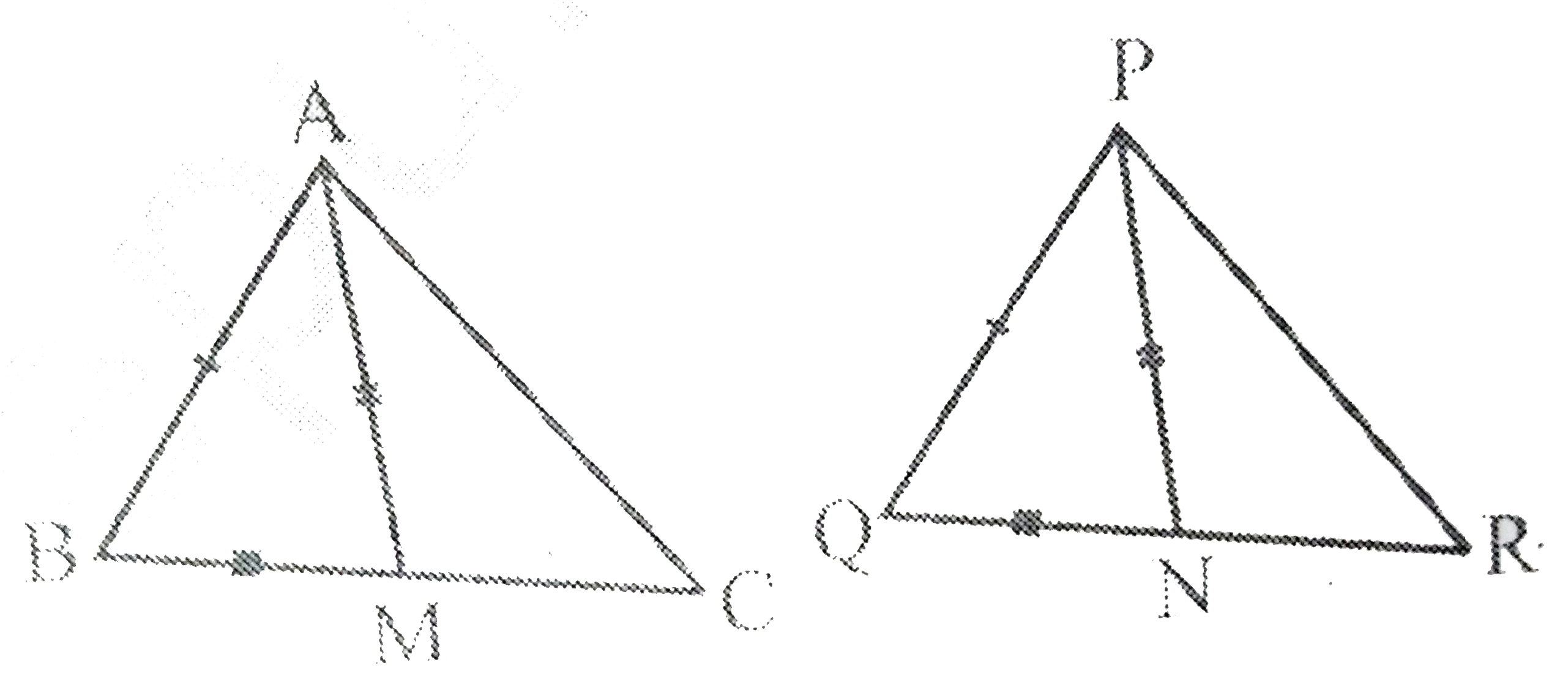
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

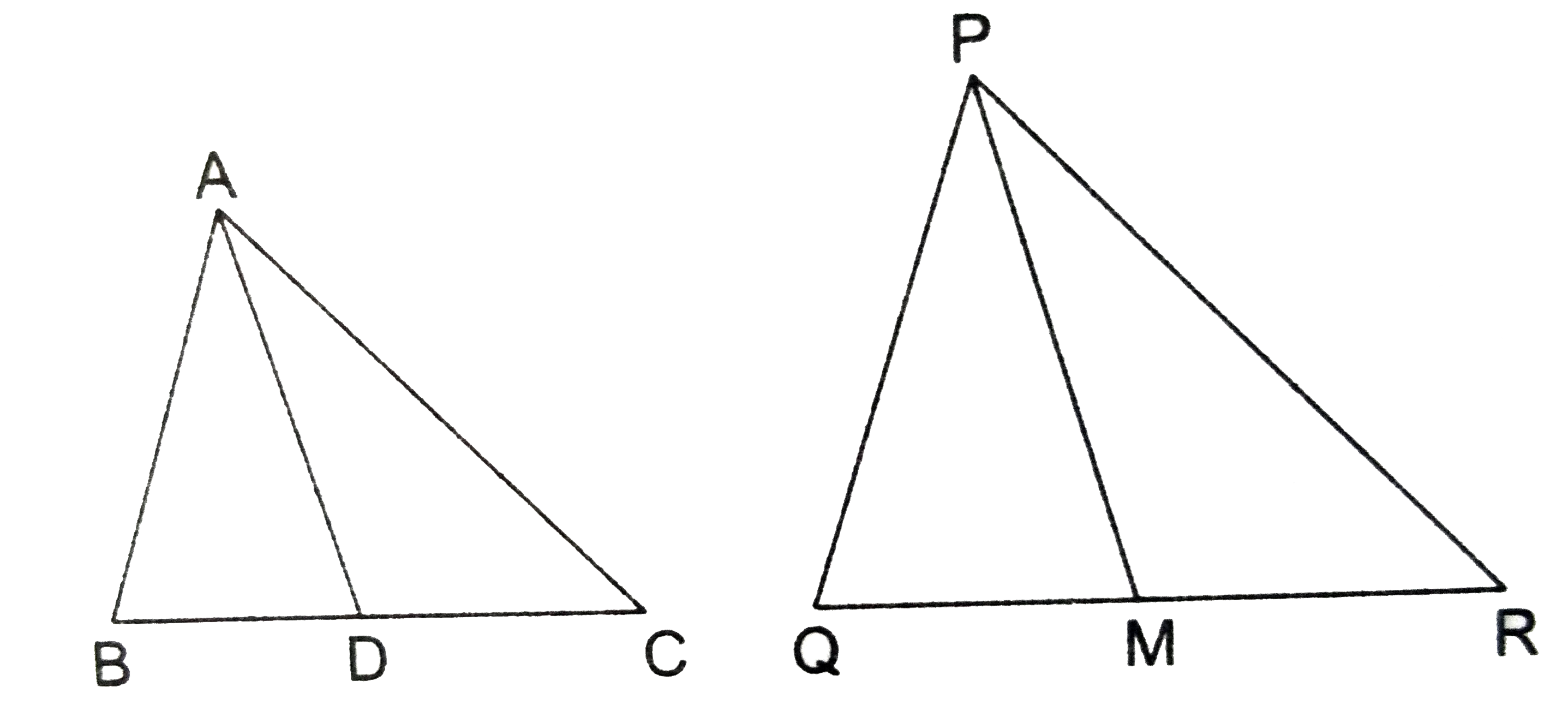
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to side PQ and QR and median PN of ΔABC≅ΔPQR(see Fig. 7.40). Show that:
(i) ΔABM≅ΔPQN
(ii) ΔABC≅ΔPQR
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution
