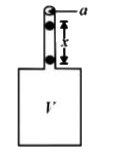
An air chamber of volume V has a neck of cross-sectional area a into which a light ball of mass m just fits and can move up and down without friction. Consider diameter of the ball to be equal to that of the neck of the chamber. The ball is then pressed down a little and released. Let the bulk modulus of air is B. The time period of the oscillation of the ball is:

$T = 2 π \sqrt{\frac{B a^{2}}{m V}}$

$T = 2 π \sqrt{\frac{B V}{m a^{2}}}$

$T = 2 π \sqrt{\frac{m B}{V a^{2}}}$

$T = 2 π \sqrt{\frac{m V}{B a^{2}}}$

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

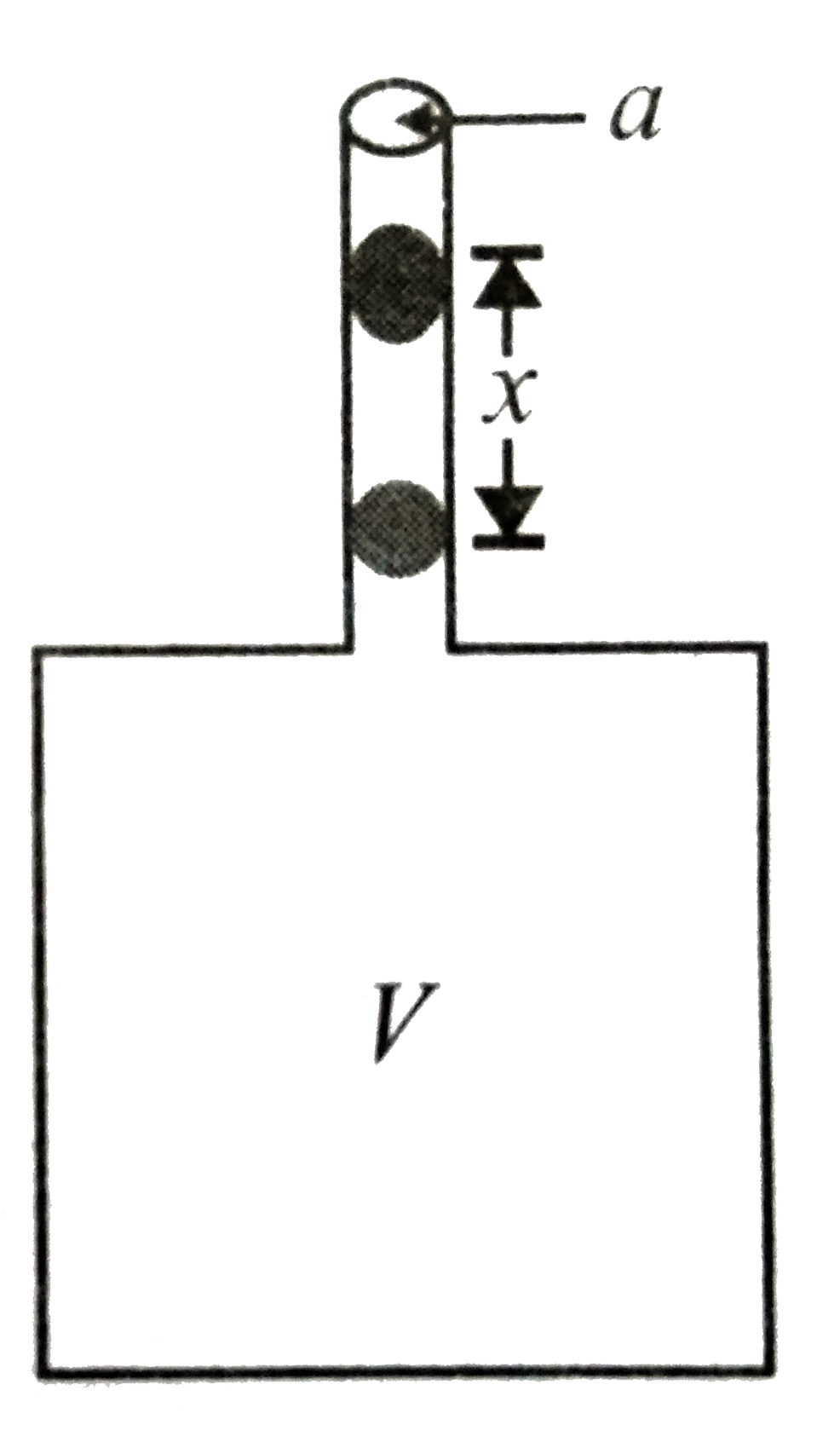
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
A $T = 2 π \sqrt{\frac{B a^{2}}{m V}}$
B $T = 2 π \sqrt{\frac{B V}{m a^{2}}}$
C $T = 2 π \sqrt{\frac{m B}{V a^{2}}}$
D $T = 2 π \sqrt{\frac{m V}{B a^{2}}}$
An air chamber of volume $V$ has a long of cross sectional area $A$ . A ball of mass $m$ is fixed sympthlly in the track The ball modulus of air is $B$ ball is pressed down slightly and released, the time period of the oscillation is
A $2 π \sqrt{\frac{m V}{2 B A^{2}}}$
B $π \sqrt{\frac{2 m V}{B A^{2}}}$
C $2 π \sqrt{\frac{m V}{B A^{2}}}$
D $\frac{π}{2} \sqrt{\frac{m}{B A^{2}}}$
A cubical ball is taken to a depth in volume observed to be $0.1 %$ the bulk modulus of the ball is $(g = 10 m / s^{2})$
A $2 \times 10^{7} P a$
B $2 \times 10^{6} P a$
C $2 \times 10^{9} P a$
D $1.2 \times 10^{9} P a$