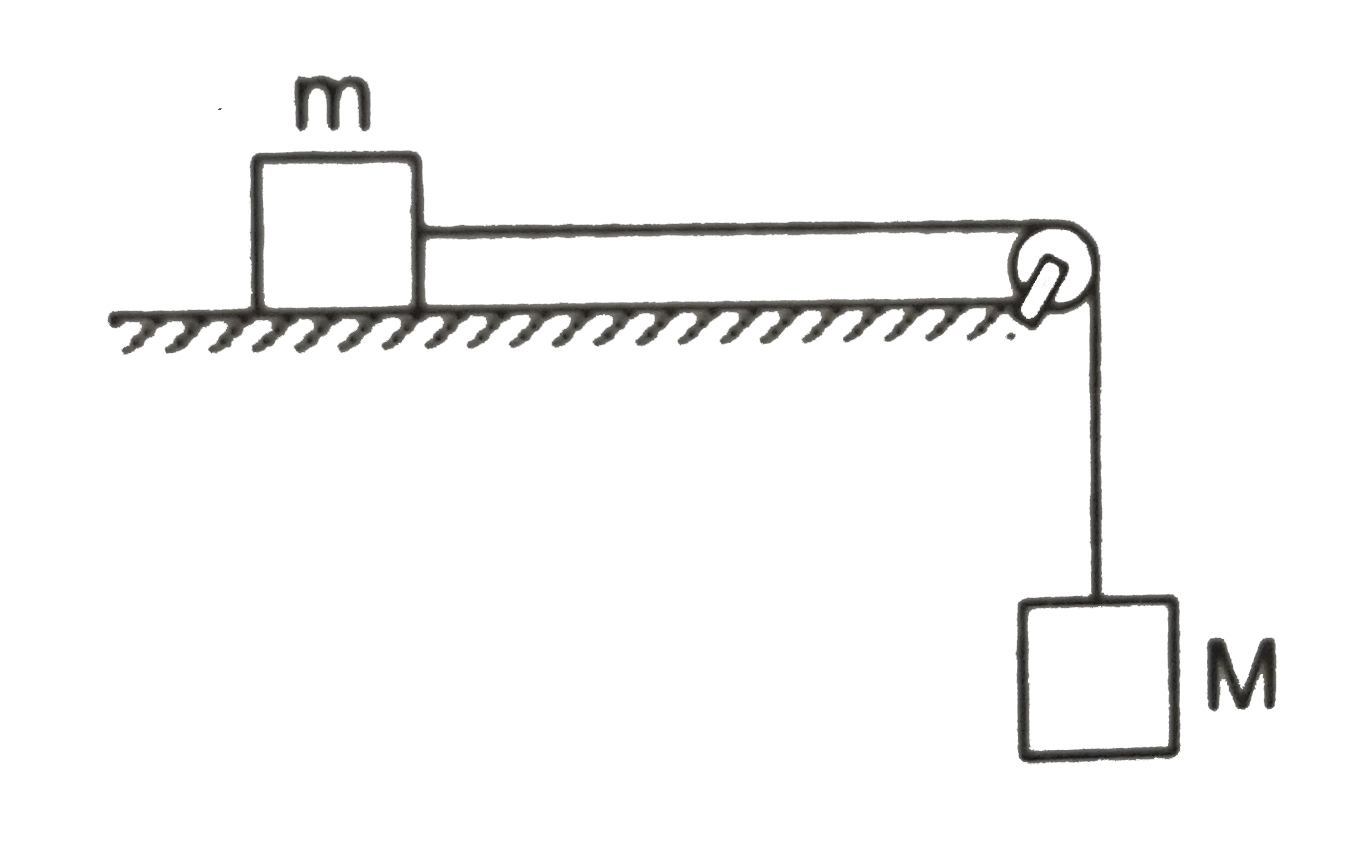
Explain the motion of an object suspended by a cable that passes over a pulley and horizontally connected at the other end to a second object that rests on a smooth horizontal table. Derive expressions for tension in the cable and acceleration of the objects.
To analyze the motion of an object suspended by a cable over a pulley, connected to another object resting on a smooth horizontal table, we can derive expressions for the tension in the cable and the acceleration of the objects. Let's denote the masses as follows:
- Let m1 be the mass of the object on the table.
- Let m2 be the mass of the object hanging off the table.
Step 1: Identify Forces Acting on Each Mass
1. For mass m2 (the hanging mass):
- The downward force due to gravity is m2g.
- The upward force due to tension in the cable is T.
- The net force acting on m2 can be expressed as:
m2g−T=m2a(1)
where a is the acceleration of the system.
2. For mass m1 (the mass on the table):
- The only horizontal force acting on m1 is the tension T.
- The net force acting on m1 can be expressed as:
T=m1a(2)
Step 2: Set Up the Equations
From the two equations derived above, we have:
1. From equation (1):
m2g−T=m2a
2. From equation (2):
T=m1a
Step 3: Substitute for Tension
Substituting equation (2) into equation (1):
m2g−m1a=m2a
Step 4: Solve for Acceleration
Rearranging the equation gives:
m2g=m1a+m2a
m2g=(m1+m2)a
Now, solving for a:
a=m2gm1+m2(3)
Step 5: Solve for Tension
Now, substitute a from equation (3) back into equation (2) to find T:
T=m1a=m1(m2gm1+m2)
Thus, we have:
T=m1m2gm1+m2(4)
Final Expressions
1. The acceleration of the system is:
a=m2gm1+m2
2. The tension in the cable is:
T=m1m2gm1+m2
- Let m2 be the mass of the object hanging off the table.
- The downward force due to gravity is m2g.
- The upward force due to tension in the cable is T.
- The net force acting on m2 can be expressed as:
m2g−T=m2a(1)
where a is the acceleration of the system.
- The only horizontal force acting on m1 is the tension T.
- The net force acting on m1 can be expressed as:
T=m1a(2)
m2g−T=m2a
T=m1a
m2g−m1a=m2a
m2g=m1a+m2a
m2g=(m1+m2)a
Now, solving for a:
a=m2gm1+m2(3)
T=m1a=m1(m2gm1+m2)
Thus, we have:
T=m1m2gm1+m2(4)
a=m2gm1+m2
T=m1m2gm1+m2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - SHORT ANSWER TYPE QUESTION
7 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
13 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
Consider two objects of different masses connected by a cable passing over a massless and frictionless Pulley. Derive expressions for the tension in the cable and acceleration of the objects.
View SolutionTwo blocks of masses 2 kg and 4 kg are connected by a light string passing over a light smooth pulley clamped to the edge of a horizontal table. The 2 kg block is on the smooth horizontal table and the other block is hanging vertically, (i) Find the acceleration of the stem if it is released from rest, (ii) Find the tension in the string.
View Solution
Knowledge Check
One end of string of length l is connected to a particle on mass m and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed v the net force on the particle (directed toward centre) will be (T reprents the tension in the string):
ATBT−(mv)2lCT+mv2lD0
A block of mass 1kg is tied to a string of length 1m the other end of which is fixed The block is moved on a smooth horizontal table with constant speed 10ms−1. Find the tension in the string
View SolutionFigure shows two blocks of masses m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
View SolutionA cat of mass m = 1 kg climbs to a rope hung over a leight frictionless pulley. The opposite end of the rope is tied to a weight of mass M = 2m lying on a smooth horizontal plane. What is the tension of the rope when the cat move upwards with in acceleration a=2m/s2 relative to the rope ?

View SolutionUniform rod AB is hinged at the end A in the figure. The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless. Masses of the block and the rod are same and are equal to 'm'. Acceleration due to gravity is g. The tension in the thread and angular acceleration of the rod just after releases of block from this position are

View SolutionA 2 kg block A is attached to one end of a light string that passes over an an ideal pulley and a 1 kg sleeve B slides down the other part of the string with an acceleration of 5m/s2 with respect to the string. Find the acceleration of the block, acceleration of sleeve and tension in the steing. [g=10m/s2]

View SolutionOne end of string of length l is connected to a particle on mass m and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed v the net force on the particle (directed toward centre) will be (T reprents the tension in the string):
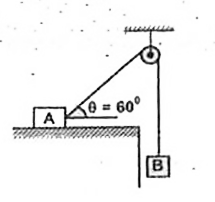
View SolutionTwo blocks A & B are connected by a light inextensible string passing over a fixed smooth pulley as shown in the figure. The coefficient of friction between the block A and the horizontal table is μ=0.2. If the block A is just to slip, find the ratio of the masses of the blocks.
View Solution
