A parallel plate capacitor (condenser) has a certain capacitance (capacity). When 2/3 rd of the distance between the plates is filled with a dielectric, the (capacity) capacitance is found to be 2.25 times the initial capacitance. The dielectric constant of the dielectric
1
3
7
6
The correct Answer is:D
To solve the problem of finding the dielectric constant k of a dielectric material that fills 23 of the distance between the plates of a parallel plate capacitor, we can follow these steps:
Step 1: Understand the initial capacitance
The initial capacitance C of a parallel plate capacitor with air (or vacuum) between the plates is given by:
C=Aϵ0d
where A is the area of the plates, ϵ0 is the permittivity of free space, and d is the distance between the plates.
Step 2: Define the new configuration
When 23 of the distance d is filled with a dielectric of dielectric constant k, the capacitor can be thought of as two capacitors in series:
1. Capacitor C1 (with dielectric) has a distance of 23d.
2. Capacitor C2 (without dielectric) has a distance of 13d.
Step 3: Calculate the capacitances of the two sections
The capacitance of C1 is:
C1=Akϵ023d=3Akϵ02d
The capacitance of C2 is:
C2=Aϵ013d=3Aϵ0
Step 4: Use the formula for capacitors in series
The total capacitance C′ of the two capacitors in series is given by:
1C′=1C1+1C2
Substituting the values of C1 and C2:
1C′=2d3Akϵ0+13Aϵ0
Step 5: Find a common denominator
The common denominator is 3Akϵ0:
1C′=2d+kd3Akϵ0=(2+k)d3Akϵ0
Thus,
C′=3Akϵ0(2+k)d
Step 6: Relate the new capacitance to the initial capacitance
According to the problem, the new capacitance C′ is 2.25 times the initial capacitance C:
C′=2.25C
Substituting the expression for C′:
3Akϵ0(2+k)d=2.25⋅Aϵ0d
Step 7: Simplify the equation
Cancel Aϵ0/d from both sides:
3k2+k=2.25
Step 8: Solve for k
Cross-multiplying gives:
3k=2.25(2+k)
Expanding the right side:
3k=4.5+2.25k
Rearranging:
3k−2.25k=4.5⟹0.75k=4.5
Thus,
k=4.50.75=6
Final Answer
The dielectric constant k is 6.
---
The initial capacitance C of a parallel plate capacitor with air (or vacuum) between the plates is given by:
C=Aϵ0d
where A is the area of the plates, ϵ0 is the permittivity of free space, and d is the distance between the plates.
When 23 of the distance d is filled with a dielectric of dielectric constant k, the capacitor can be thought of as two capacitors in series:
1. Capacitor C1 (with dielectric) has a distance of 23d.
2. Capacitor C2 (without dielectric) has a distance of 13d.
The capacitance of C1 is:
C1=Akϵ023d=3Akϵ02d
The capacitance of C2 is:
C2=Aϵ013d=3Aϵ0
The total capacitance C′ of the two capacitors in series is given by:
1C′=1C1+1C2
Substituting the values of C1 and C2:
1C′=2d3Akϵ0+13Aϵ0
The common denominator is 3Akϵ0:
1C′=2d+kd3Akϵ0=(2+k)d3Akϵ0
Thus,
C′=3Akϵ0(2+k)d
According to the problem, the new capacitance C′ is 2.25 times the initial capacitance C:
C′=2.25C
Substituting the expression for C′:
3Akϵ0(2+k)d=2.25⋅Aϵ0d
Cancel Aϵ0/d from both sides:
3k2+k=2.25
Cross-multiplying gives:
3k=2.25(2+k)
Expanding the right side:
3k=4.5+2.25k
Rearranging:
3k−2.25k=4.5⟹0.75k=4.5
Thus,
k=4.50.75=6
The dielectric constant k is 6.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )108videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Find the capacitance of a capacitor in which the space between the plates is partly filled with a dielectric (Fig. 25.5)
 View Solution
View SolutionA parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Assertion: The distance between the parallel plates of a capacitor is halved, then its capacitance is doubled.
Reason: The capacitance depends on the introduced dielectric.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false. - Question 2 - Select One
A parallel plate capacitor with air between the plates has a capacitance of 10 pF. The capacitance, if the distance bgetween the plates is reduced by half and the space between tehm is filled with a substance of dielectric constant 4 is
A80pFB96pFC100pFD120pF
A parallel plate capacitor has plate area A and plate separation d. The space betwwen the plates is filled up to a thickness x (ltd) with a dielectric constant K. Calculate the capacitance of the system.
 View Solution
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionTwo identical parallel plate (air) capacitors c1andc2 have capacitances C each. The space between their plates is now filled with dielectrics as shown. If two capacitors still have equal capacitance, obtain the relation betweenn dielectric constants k,k1andk2.
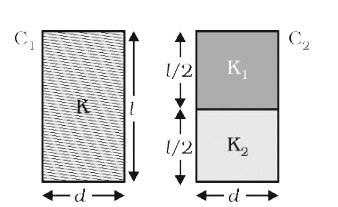 View Solution
View SolutionAn air filled parallel capacitor has capacity of 2pF. The separation of the plates is doubled and the interspaces between the plates is filled with wax. If the capacity is increased to 6pF, the dielectric constant of was is
View SolutionA parallel plate capacitor of capacitance has spacing between two plates having area The region between the plates is filled with dielectric layers, parallel to its plates, each with thickness δ=dN. The dielectric constant of the mth layer is Km=K(1+mN). For a very large N(>103), the capacitance Cisα(K∈0Adln2). Find the value of α.[∈0 is the permittivity of free space]
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View Solution
