The time in seconds required to produce a potential difference of 20V across a capacitor of 1000μ F when it is charged at the steady rate of 200μC/s is
50
100
150
200
The correct Answer is:B
To solve the problem, we need to find the time required to produce a potential difference of 20V across a capacitor of 1000 µF when charged at a steady rate of 200 µC/s.
1. Convert the given values to standard units:
- The capacitance C is given as 1000μF.
C=1000μF=1000×10−6F=10−3F
- The potential difference V is given as 20V.
- The rate of charge dqdt is given as 200μC/s.
dqdt=200μC/s=200×10−6C/s=2×10−4C/s
2. Calculate the total charge Q required to produce the potential difference:
- Using the formula Q=C×V:
Q=C×V=(10−3F)×(20V)=20×10−3C=2×10−2C
3. Calculate the time t required to charge the capacitor:
- The time can be calculated using the formula:
t=Qdqdt
- Substituting the values:
t=2×10−2C2×10−4C/s=22×102s=102s=100s
4. Conclusion:
- The time required to produce a potential difference of 20V across the capacitor is 100seconds.
Final Answer:
The time required is 100 seconds.
- The capacitance C is given as 1000μF.
C=1000μF=1000×10−6F=10−3F
- The potential difference V is given as 20V.
- The rate of charge dqdt is given as 200μC/s.
dqdt=200μC/s=200×10−6C/s=2×10−4C/s
- Using the formula Q=C×V:
Q=C×V=(10−3F)×(20V)=20×10−3C=2×10−2C
- The time can be calculated using the formula:
t=Qdqdt
- Substituting the values:
t=2×10−2C2×10−4C/s=22×102s=102s=100s
- The time required to produce a potential difference of 20V across the capacitor is 100seconds.
The time required is 100 seconds.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )108videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Calculate energy stored in a capacitor of 5μF when it is charged to a potential of 250 volt.
View SolutionFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
View SolutionIn the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
View SolutionIf A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionTwo capacitor of capacitance 2μFand3μF respectively are charged to potential difference 20 V each. Now the capacitors are connected such that the positively chargd plate of one capacitory is connected to the negatively charged plate of the other. after the current in the circuit has become negligible, the potential difference across the 2μF capacitor is ____V.
View SolutionIn the arrangement shown in , the switch S is find
 the final potential difference across the 4μF capacitorView Solution
the final potential difference across the 4μF capacitorView SolutionThree identical charged capacitors each of capacitance 5 μF are connected as shown in figure. Potential difference across capacitor (3), long time after the swithces K1andK2 are closed , is
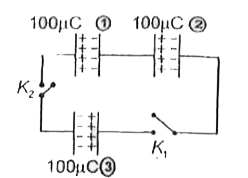 View Solution
View SolutionA capacitor when charged by a potential difference of 200 Volts, stores a charge of 0.1C. By discharging energy liberated by the capacitor is-
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum isView SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum isView Solution
