In a metere bridge, the balance length from left end (standard resistance of 1Ω is in theright gap) is found to be 20cm the length of resistance in left gap is 1/2 m and radius is 2mm its specific resistance is
π×10−6ohm−m
2π×10−6ohm−m
π2×10−6ohm−m
3π×10−6ohm−m
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the given data
- Balancing length from the left end (l1) = 20 cm = 0.2 m
- Length of resistance in the left gap (l) = 0.5 m
- Radius of the wire (r) = 2 mm = 2 × 10^-3 m
- Standard resistance in the right gap (r2) = 1 Ω
Step 2: Calculate the balancing length from the right end
The total length of the meter bridge is 100 cm (1 m). Thus, the balancing length from the right end (l2) can be calculated as:
l2=100 cm−l1=100 cm−20 cm=80 cm=0.8 m
Step 3: Use the meter bridge formula
According to the meter bridge principle:
r1r2=l1l2
Where:
- r1 = resistance in the left gap
- r2 = standard resistance in the right gap
Rearranging the formula to find r1:
r1=l1l2×r2
Step 4: Substitute the values
Substituting the known values:
r1=0.2 m0.8 m×1 Ω=14 Ω=0.25 Ω
Step 5: Calculate the cross-sectional area (A) of the wire
The cross-sectional area A of the wire is given by:
A=πr2
Substituting the radius:
A=π(2×10−3 m)2=π(4×10−6 m2)=4π×10−6 m2
Step 6: Use the formula for specific resistance (ρ)
The resistance r1 is also given by the formula:
r1=ρlA
Rearranging to find the specific resistance ρ:
ρ=r1⋅Al
Step 7: Substitute the values into the specific resistance formula
Substituting the known values:
ρ=(0.25 Ω)⋅(4π×10−6 m2)0.5 m
ρ=1π×10−6 Ω m0.5=2π×10−6 Ω m
Final Answer
Thus, the specific resistance ρ is:
ρ=2π×10−6 Ω m
---
- Balancing length from the left end (l1) = 20 cm = 0.2 m
- Length of resistance in the left gap (l) = 0.5 m
- Radius of the wire (r) = 2 mm = 2 × 10^-3 m
- Standard resistance in the right gap (r2) = 1 Ω
The total length of the meter bridge is 100 cm (1 m). Thus, the balancing length from the right end (l2) can be calculated as:
l2=100 cm−l1=100 cm−20 cm=80 cm=0.8 m
According to the meter bridge principle:
r1r2=l1l2
Where:
- r1 = resistance in the left gap
- r2 = standard resistance in the right gap
r1=l1l2×r2
Substituting the known values:
r1=0.2 m0.8 m×1 Ω=14 Ω=0.25 Ω
The cross-sectional area A of the wire is given by:
A=πr2
Substituting the radius:
A=π(2×10−3 m)2=π(4×10−6 m2)=4π×10−6 m2
The resistance r1 is also given by the formula:
r1=ρlA
Rearranging to find the specific resistance ρ:
ρ=r1⋅Al
Substituting the known values:
ρ=(0.25 Ω)⋅(4π×10−6 m2)0.5 m
ρ=1π×10−6 Ω m0.5=2π×10−6 Ω m
Thus, the specific resistance ρ is:
ρ=2π×10−6 Ω m
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (ELECTRIC POTENTIAL & CAPACITANCE )143videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Knowledge Check
- Question 1 - Select One
In a meter bridge experiment the ratio of left gap resistance to right gap resistance is 2:3 the balance point from is
A60cmB50cmC40cmD20cm - Question 2 - Select One
Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
A3B6C9D12
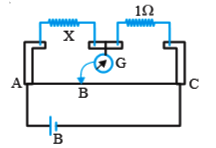
In the metre bridge, the balancing length AB =l=20 cm. The unknown resistance X is equal to
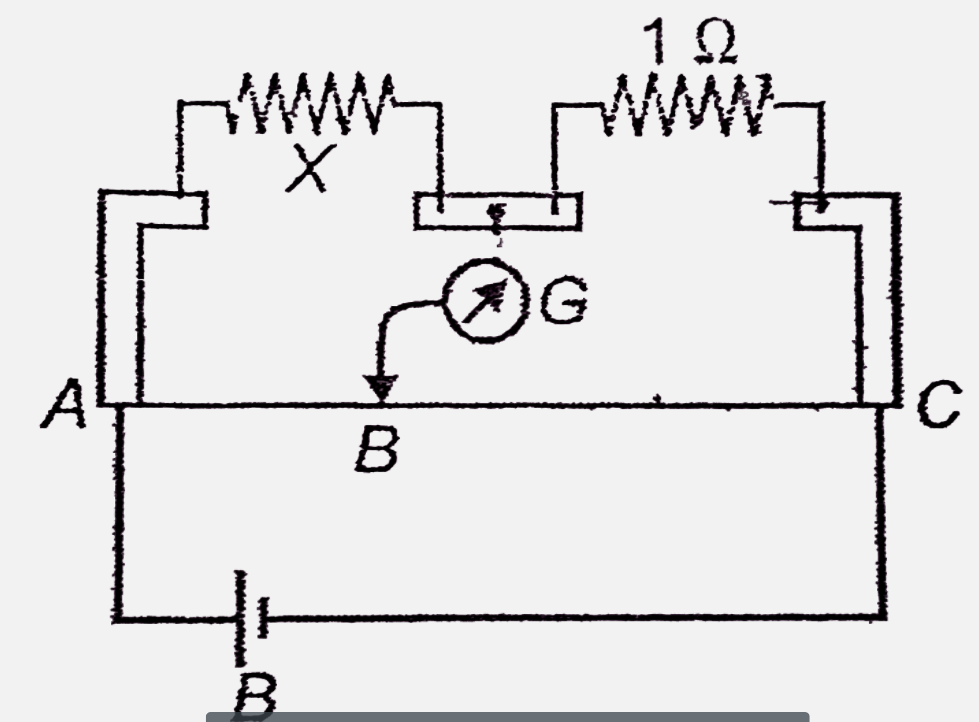 View Solution
View SolutionIn a potentiometer experiment, the balancing length with a resistance of 2Ω is found to be 100cm, while that of an unknown resistance is 500cm. Calculate the value of the unknown resistance.
View SolutionThe resistance in two arms of the meter bridge is 10Ω and x respectively. The balance length is l1from left. Now the resistance of 10Ω is shunted with another resistor of resistance equal to unknown resistance x then new balance point is 0.75l1 The value of resistance x is
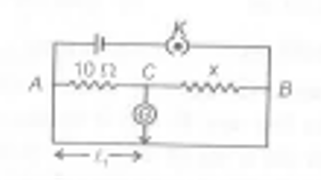 View Solution
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
View SolutionTwo resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View Solution