A spherically symmetric gravitational system of particles has a mass density ρ={ρ0r≤R0r>R where ρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed as a function of distances r (0<r<∞) from the centre of the system is represented by Solution in Punjabi
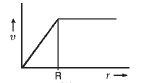
Step by step video & image solution for A spherically symmetric gravitational system of particles has a mass density rho={(rho_0, rleR),(0, rgt R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed as a function of distances r (0 <r<infty) from the centre of the system is represented by by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
What are the three modes of transfer of heat ?
View SolutionA steel wire of length 4.7 m and cross-sectional area 3.0×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0×10−5M2 under a given load. What is the ratio of the Young’s modulus of steel to that of copper?
View SolutionA spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by
View SolutionConsider a spherical gaseous cloud of mass density rho(r) in a free space where r is the radial distance from its centre. The gaseous cloud is made of particle of equal mass m moving in circular orbits about their common centre with the same kinetic energy K. The force acting on the particles is their mutual gravitational force. If rho(r) is constant with time. the particle number density n(r)= rho(r) /m is : (G=universal gravitational constant)
View Solutionएक गोलाकार सममित (symmetrical) गुरुत्वीय के समूह का द्रव्यमान घनत्व ρ={ρ0r<R के लिए 0r>R के लिए }, जहाँ ρ0 एक अचल है |
समूह के केन्द्र r(0<r<∞) दूरी पर एक परीक्षण द्रव्यमान, कणो के गुरुत्वीय क्षेत्र के प्रभाव में वृत्तीय गति करता है | इसकी गति v को r के सापेक्ष किस प्रकार से दर्शाया जायेगा ?
View SolutionThe volume charge density in a spherical ball of radius R varies with distance r from the centre s ρ(r)=ρ0[1−(rR)3] where ρ0 is a constant. The radius at which the field be maximum is
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
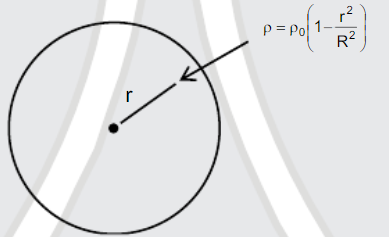
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field

View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionLet there be a spherically symmetric charge distribution with charge density varying as ρ(r)=ρ0(54−rR) upto r = R, and ρ(r)=0 for r >R, where r is the distance from the origin. The electric field at a distance r (r
View SolutionA spherically symmetric charge distribution is characterized by a charge density having the following variation : ρ(r)=ρ0forr<Rρ(r)=0 for r≥ R. Where r is the distance from the centre of the charge distribution and pois a constant. The electric field at an internal point (r
View Solutionएक गोलाकार सममित (symmetric) गुरूत्वीय कणों के समूह का द्रव्यमान घनत्व ρ={ρ0 for r≤R0 for r>R जहाँ ρ0 एक स्थिरांक है। कणों के गुरूत्वीय क्षेत्र के प्रभाव में एक परीक्षण आवेश वृत्तीय गति कर रहा है। निकाय के केन्द्र से r दूरी r(0<r<∞) पर इसकी चाल होगी।
View SolutionA spherically symmetric gravitational system of particles has a mass density rho={(rho_0,for, r,lt,R),(0,for,r,gt,R):} where rho_0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0ltrltOO) form the centre of the system is represented by
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionA spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
View Solution
