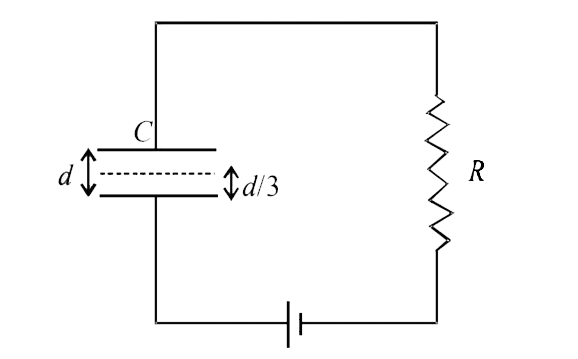
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-
6ε0R5d+3Vt
(15d+9Vt)ε0R2d2−3dVt−9V2t2
6ε0R5d−3Vt
(15d−9Vt)ε0R2d2+3dVt−9V2t2
The correct Answer is:A
A = 1, Separation = d
k=2,t=d3
Let level of liquid at any instant of time .t. be x.
V=−dxdt⇒dx=−Vdt
⇒∫xd3dx=−V∫t0dt⇒x−d3=−Vt
⇒x=d3−Vt
Now, 1Ceq=1C1+1C2
⇒Ceq=C1×C2C1+C2=(Aε0d−x)×(ε0Akx)Aε0(d−x)+ε0Akx
⇒Ceq=kAε0kd+x(1−k)
⇒Ceq=2ε02d+(d3−Vt)(1−2)=2ε02d−d3+Vt
=6ε05d+3Vt
Time constant τ=RCeq=6ε0R5d+3Vt
Similar Questions
A parallel plate capacitor with a liquid filled between the plates (dielectric constant of liquid, K = 4) has capacitance 20μF. If the liquid is removed then capacitance of capacitor becomes
View SolutionA parallel plate capacitor with liquid filled between the plates (dielectric constant of liquid, k=4)has capacitance 20μF. If the liquid is removed then capacitance of capacitor becomes
View SolutionA parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K=2. The level of liquid is d/3 initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time t is-

View SolutionA parallel plate capacitor with liquid filled between the plates (dielectric constant of liquid, k=4)has capacitance 20μF. If the liquid is removed then capacitance of capacitor becomes
View SolutionFind an expression for the capacitance of a parallel plate capacitor when a dielectric slab of dielectric constant K and thickness t=(d)/(2) but the same area on the plates is inserted between the the capacitors plate. (d=separation between the plates)
View SolutionCapacitance of a parallel plate capacitor becomes 43 times its original value if a dielectric slab of thickness t = d2 is inserted between the plates (d is the separation the plates). The dielectric constant of the slab is
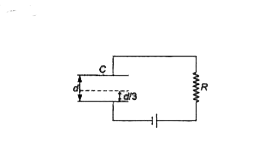
View SolutionA parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K =2, the level of liquid is d3, intially, Suppose the liquid , level decreases at a constant speed v, the time constant as a function of time is
View SolutionA parallel plate capacitor has plate separation d and the area of each plate is A. The space between the plates is completely filled with a dielectric constant K. Derive the expression for the capacity of the parallel plate capacitor.
View Solution
