The current density in a cylindrical wire of radius 4 mm is 4×106Am−2. The current through the outer portion of the wire between radial distances R2 and R is ______ π A
To solve the problem, we need to find the current flowing through the outer portion of a cylindrical wire between radial distances R/2 and R. Given the current density J and the radius of the wire, we can use the following steps:
Step 1: Convert the radius to meters
The radius of the wire is given as 4mm. We need to convert this to meters:
R=4mm=4×10−3m
Hint: Always convert units to the SI system for consistency in calculations.
Step 2: Identify the current density
The current density J is given as:
J=4×106A/m2
Hint: Current density is the current per unit area and is crucial for calculating the total current.
Step 3: Calculate the area for the annular section
We need to find the area of the annular section between R/2 and R. The area A of an annulus is given by the difference of the areas of two circles:
A=πR2−π(R2)2
Substituting the value of R:
A=π(4×10−3)2−π(4×10−32)2
Calculating the areas:
=π(16×10−6)−π(4×10−6)
=π(16×10−6−4×10−6)
=π(12×10−6)
Hint: The area of the annular section is found by subtracting the area of the inner circle from the area of the outer circle.
Step 4: Calculate the current through the annular section
The current I through the annular section can be calculated using the formula:
I=J×A
Substituting the values:
I=J×π(12×10−6)
=(4×106)×π(12×10−6)
=48πA
Hint: The current is directly proportional to the current density and the area through which it flows.
Final Answer
The current through the outer portion of the wire between radial distances R/2 and R is:
48πA
The radius of the wire is given as 4mm. We need to convert this to meters:
R=4mm=4×10−3m
The current density J is given as:
J=4×106A/m2
We need to find the area of the annular section between R/2 and R. The area A of an annulus is given by the difference of the areas of two circles:
A=πR2−π(R2)2
Substituting the value of R:
A=π(4×10−3)2−π(4×10−32)2
Calculating the areas:
=π(16×10−6)−π(4×10−6)
=π(16×10−6−4×10−6)
=π(12×10−6)
The current I through the annular section can be calculated using the formula:
I=J×A
Substituting the values:
I=J×π(12×10−6)
=(4×106)×π(12×10−6)
=48πA
The current through the outer portion of the wire between radial distances R/2 and R is:
48πA
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A
19 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A (ASSERTION (A) REASON (R))
1 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
(a) The current density in a cylindrical wire of radius R=2.0mm is uniform across a cross section of the wire and is J=2.0×105A/m2. What is the current through the outer portion of the wire between radial distances R/2 and R?
(b) Suppose, instead, the current density through a cross section varies with radial distance r as J=ar2, in which a=3.0×1011A/m4 and r is in meters. What now is the current through the same outer portion of the wire?
View SolutionA cylindrical wire if radius R = 2 mm is of uniform area of cross-section. The current density through a cross-section varies with radial distance r as J=ar2, where a=3.2×1011A/m2 and r is in metres. What is the current through the outer portion of the wire between radial distances R/2 and R?
View Solution
Knowledge Check
The current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
A65πaR42592B25πaR472C65πa2R32938DNone of theseThe current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
A65πaR42592B25πaR472C65πa2R32938D81πa2R4144A current of 2 amp. flows in a long, straight wire of radius 2mm. The intensity of magnetic field on the axis of the wire is
A(μ0π)×103 TeslaB(μ02π)×103 TeslaC(2μ0π)×103 TeslaDZero
The current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View SolutionCurrent flows through a constricted conductor as shown in figure
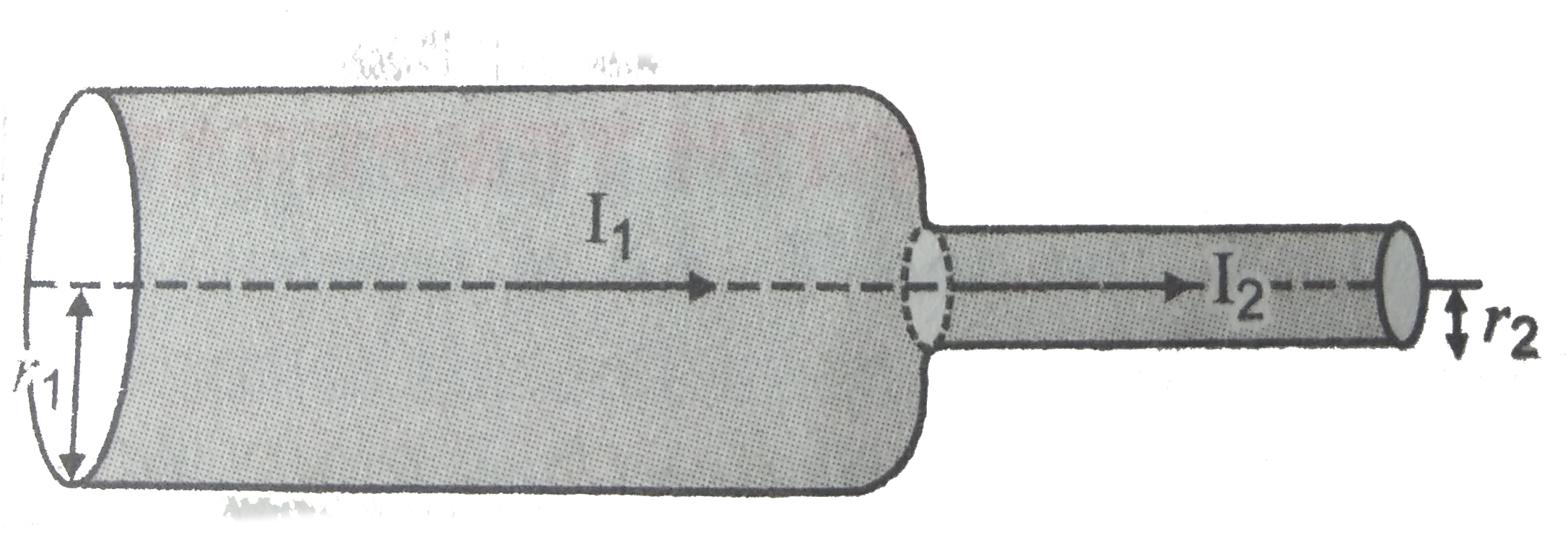
The radius and the current density to the left of constriction are 2 mm and 4.2×105Am−2. (a) How much current flows through the constriction? (b) If the current density is doubled as emerges from the right side of the constriction, what is the radius r2?
View SolutionA current of 4.8 A is flowing in a copper wire of cross-sectional area 3×10−4m2. Find the current density in the wire.
View SolutionA uniform current I is flowing in a long wire of radius R. If the current is uniformly distributed across the cross-sectional area of the wire, then
View SolutionThe current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
View Solution
