Two identical charged particles each having a mass 10 g and charge 2.0×10−7 C are placed on a horizontal table with a separation of L between them such that they stay in limited equilibrium. If the coefficient of friction between each particle and the table is 0.25, find the value of L. (Use g =10ms−2)
12 cm
10 cm
8 cm
5 cm
To find the separation L between the two identical charged particles in limited equilibrium, we need to balance the electrostatic force of repulsion with the frictional force that resists their motion.
1. Identify the Forces:
- Electrostatic force of repulsion between the two charges: Fe
- Frictional force resisting the motion: Ff
2. Electrostatic Force:
The electrostatic force between two charges q separated by a distance L is given by Coulomb's law:
Fe=kq2L2
where k is Coulomb's constant (k=9×109Nm2/C2), and q=2.0×10−7C.
3. Frictional Force:
The frictional force is given by:
Ff=μmg
where μ is the coefficient of friction (μ=0.25), m is the mass of each particle (m=10g=0.01kg), and g is the acceleration due to gravity (g=10m/s2).
4. Equilibrium Condition:
For the particles to be in limited equilibrium, the electrostatic force must be equal to the frictional force:
Fe=Ff
5. Substitute the Forces:
kq2L2=μmg
6. Solve for L:
9×109×(2.0×10−7)2L2=0.25×0.01×10
Simplify the right-hand side:
0.25×0.01×10=0.025
Now, equate and solve for L2:
9×109×4×10−14L2=0.025
36×10−5L2=0.025
36×10−50.025=L2
L2=36×10−50.025
L2=36×10−525×10−3
L2=36×10−525×10−3=3625×10−2
L2=1.44×10−2
L=√1.44×10−2
L=0.12m
7. Convert to Centimeters:
L=0.12m=12cm
Final Answer:
The separation L between the two charged particles is 12cm.
- Electrostatic force of repulsion between the two charges: Fe
- Frictional force resisting the motion: Ff
The electrostatic force between two charges q separated by a distance L is given by Coulomb's law:
Fe=kq2L2
where k is Coulomb's constant (k=9×109Nm2/C2), and q=2.0×10−7C.
The frictional force is given by:
Ff=μmg
where μ is the coefficient of friction (μ=0.25), m is the mass of each particle (m=10g=0.01kg), and g is the acceleration due to gravity (g=10m/s2).
For the particles to be in limited equilibrium, the electrostatic force must be equal to the frictional force:
Fe=Ff
kq2L2=μmg
9×109×(2.0×10−7)2L2=0.25×0.01×10
Simplify the right-hand side:
0.25×0.01×10=0.025
Now, equate and solve for L2:
9×109×4×10−14L2=0.025
36×10−5L2=0.025
36×10−50.025=L2
L2=36×10−50.025
L2=36×10−525×10−3
L2=36×10−525×10−3=3625×10−2
L2=1.44×10−2
L=√1.44×10−2
L=0.12m
L=0.12m=12cm
The separation L between the two charged particles is 12cm.
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)20videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)10videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS60videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )10videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question360videos
JEE MAINS 2023 JAN ACTUAL PAPER
Similar Questions
Two particles, each having a mass of 5 gm and charge 1.0×10−7C, stay in limiting equilirbium on a horizontal table with a separation of 10 cm between them. The coefficient of friction between each particle and the table is the same. Find the value of this coefficient.
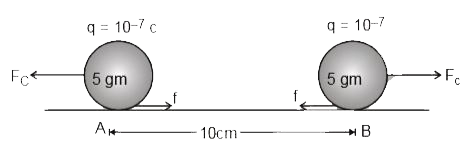 View Solution
View SolutionTwo particles, each having a mass of 5 g and charge. 1.0×10−7 C, stay in limiting wquilibrium on a horizontal. table with a seaprtion of 10 cm between them. The coefficient of friction beteen each partcle and the table. is the same. Find the value of this coefficient.
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
ABy the applied force is 150 JBBy the frictional force is 60 JCBy the applied force and the net force are 150 J and 90 J respectivelyDAll are correct
Two identical particles, each having a charge of 2.0×10−4C and then released. What would be the speeds of the particles when the separtion becomes large?
View SolutionThe fricition coefficient between the table and block shown in fig. is 0.2 find the acceleration of the system (Take g=10m/s2)
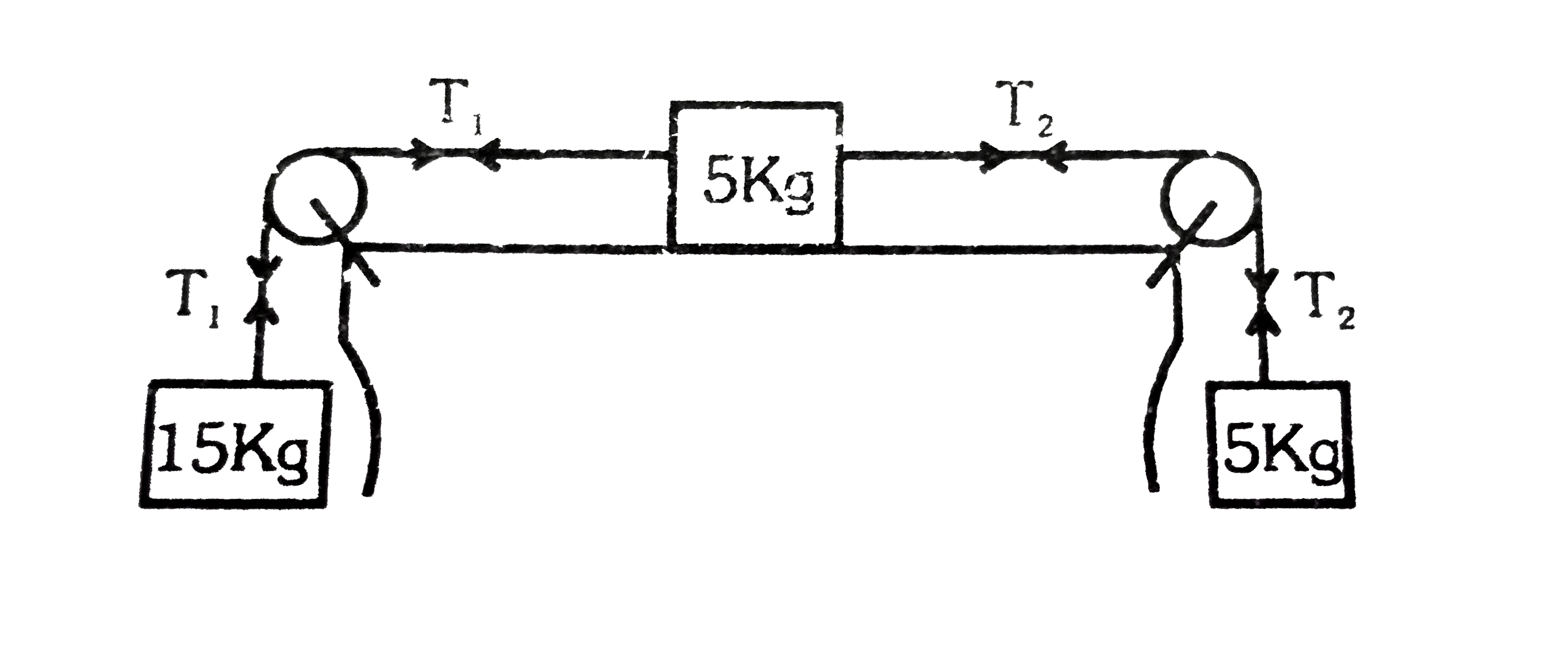 View Solution
View SolutionTwo charged particles, having equal charges of 2.0×10−5C each, are brought from infinity to within a separation of 10 cm. Find the increase in the electric potential energy during the process.
View SolutionTwo charges particles each having equal charges 2×10−5C are brought from infinity to within a separation of 10 cm. Calculate the increase in potential energy during the process and the work required for this purpose.
View SolutionA particle A having a charge of 2.0×10−6C is held fixed on a horizontal table. A second charged jparticle of mass 80g stays in equilibrium on the table at a distance of 10 cm from the firsst charge. The coefficient of friction between the table and this second jparticle is μ=0.2. find the range within which the charge of this second particle may lie.
View SolutionTwo particles have equal masses of 5.0 g each and opposite charges of +4.0×10−5C. They are released from rest with a separation of 1.0 m between them. Find the speeds of the particles when the separation is reducced to 50 cm.
View SolutionTwo positively charged small particles, each of mass 1.7×10−27kg and carrying a charge of 1.6×10−19C are placed apart at a separation r. If each one experiences a repulsive force equal to its weight find their separation. [0.117 m]
View Solution

