A paticle of mass 50 g moves on a straight line. The vatiation of speed with time is shown in figure. Find the force acting on the particle at t=2,4 and 6 secons.

Video Solution

Text Solution

Verified by Experts

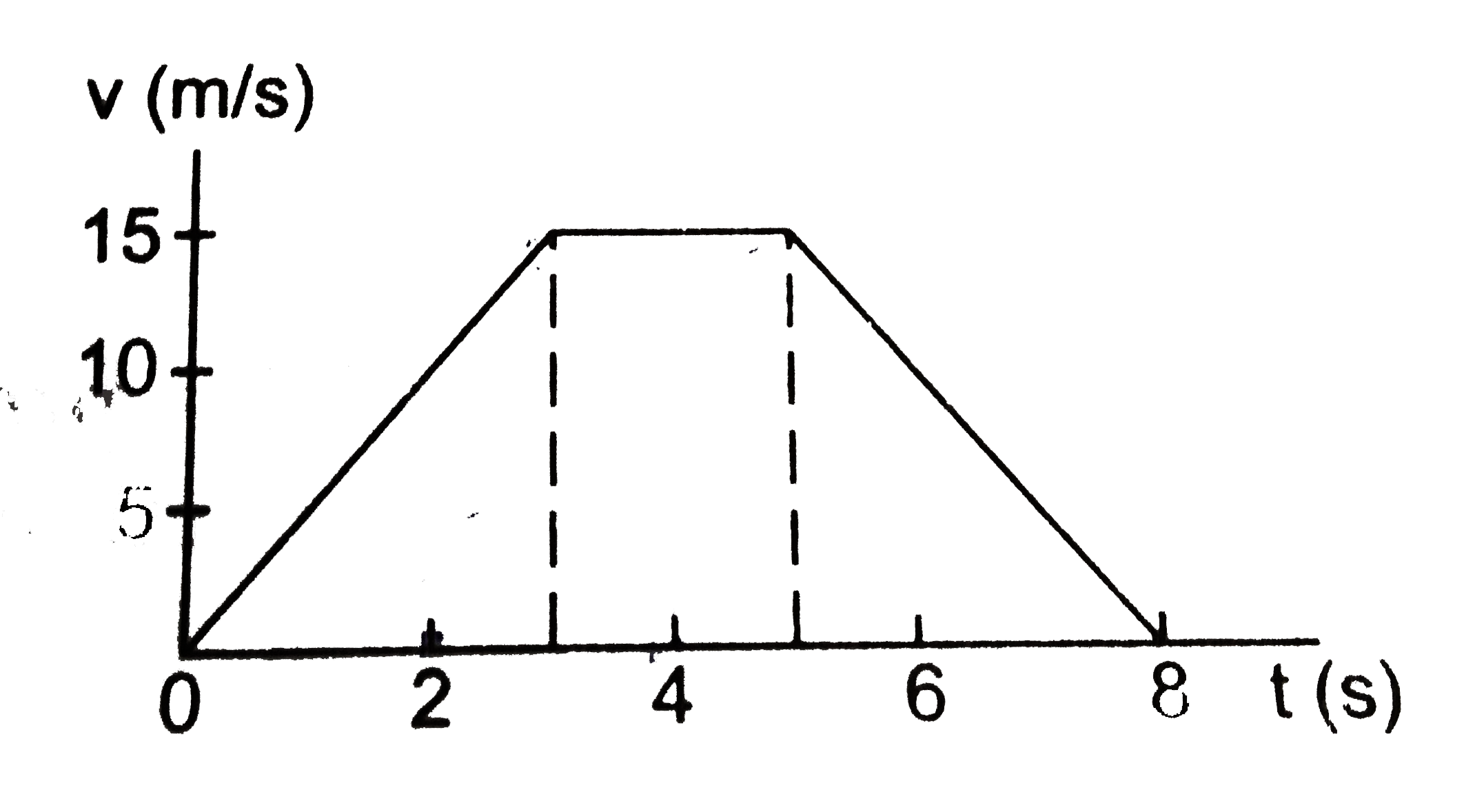
Given $m = 50 g = 5 \times 10^{- 2} k g$
As shown in the ure
Slopd of $O A = tan θ$
$= \frac{A D}{O D} = \frac{15}{3} = \frac{m}{s^{2}}$

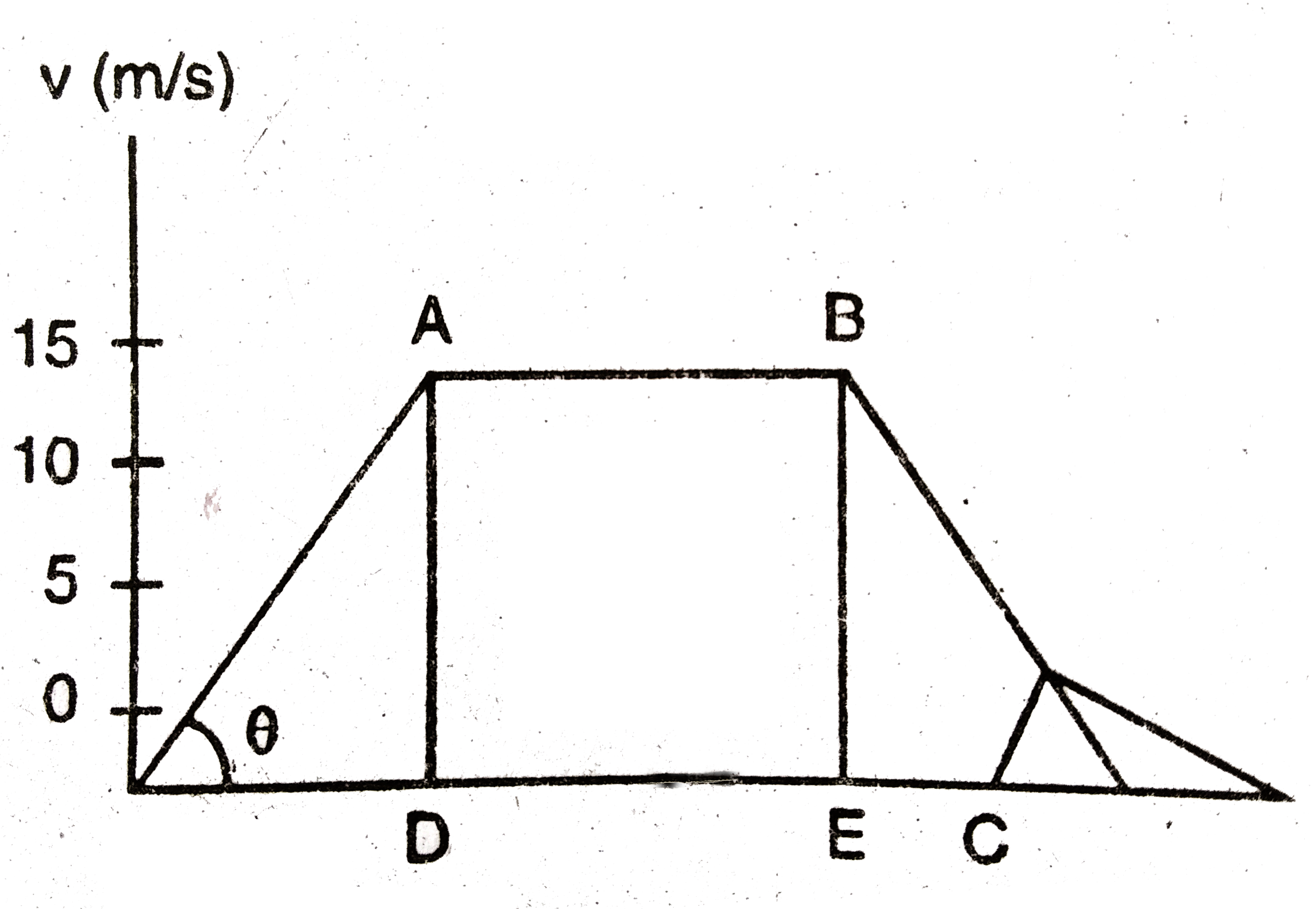
So, at t=2 sec, acceleration is 5 m/s^2
Force $= m a = 5 \times 10^{- 2} \times 5$
$= 0.25 N$ along the motion ltBrgt At $t = 4 sec$ ,
Slope of $a b = 0$
and acceleration =0 [Since $tan θ = 0^{0}]$
$t t = 6 sec$ ,
acceleration = slope of BC
$I n △ B E C, tan θ = 5$
$S l o p e o f B C = tan (108^{0} - θ) - tan θ$
$= 5 \frac{m}{s^{2}} (d e c e \leq r a t i o n) < b r >$ :. Force = ma= 5xx 10^-2 xx5 $< B r >$ =0.25 N
Opposite to the motion.

Updated on:21/07/2023

The kinetic energy of a body moving along a straight line varies with time as shown in figure. The force acting on the body:

Azero
Bconstant
Cdirectly proportional to velocity
Dinversely proportional to velocity
Kinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
ADirectly proportional to the speed of the particle
BInversely proportional to $\sqrt{t}$
CInversely proportional to the speed of the particle
DDirectly proportional to $\sqrt{t}$
A particle of mass 10 kg is moving in a straight line. If its displacement, x with time tis given by $x = (t^{3} - 2 t - 10) m$ then the force acting on it at the end of 4 seconds is
A24N
B240N
C300N
D1200N