Consider a pulley fixed at its centre of mass by a clamp. A light rope is wound over ti and the free end is tied to block. The tension in the rope is T. a. Write the frce acting on tehpulley. How are they related? B. Locate the axis of rotation. c.Find the torque f the forces abut the axis of rotation.
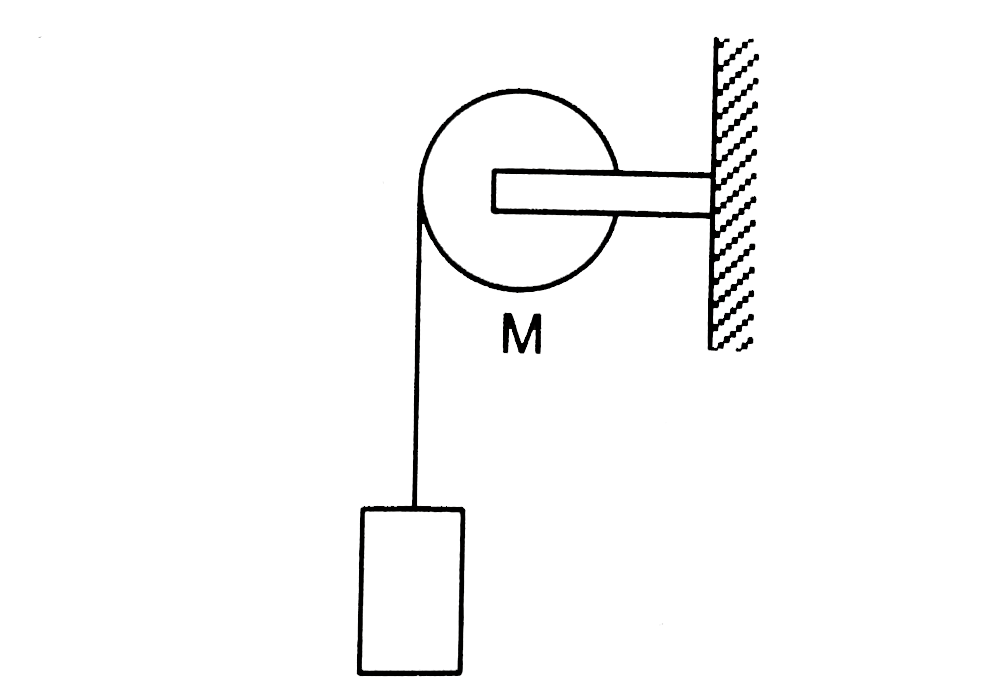
a. the forces on the pulley are ure.
i. attraction by the earth Mg vertically downward
ii tension tl by the rope along the rope
iii contact force N by the support at the centre.
N=T+Mg (centre of mass of the pulley is at rest so Newoton's 1st law applies.
b. The axis of rotation is the line through the centre of the pulley and perpendicular to theplane of the pulley.
c. Let us take the positive direction of the axis towards the reader.
The force Mg passses through the centre of mass and it intersects the axis of rotation. Hence the torque of Mg abut teh axils is zero (casse II). Similarly the torque of the contct force N is also zero.
The tension T is along the tangent of the rim in the vertically downward direction. The tension and the axis of rotation are perpendicular but never intersect. Case III applies. Join the point where the rope leaves the rim to the centre. TGhis line is the common perpendicular tot the tension and the axis. Hence the torque is T.r (positive, since it wil try to rotate the ulley anticlockwise).
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Worked Out Examples
29 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Short Answer
22 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
A 2.00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View Solution
Knowledge Check
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
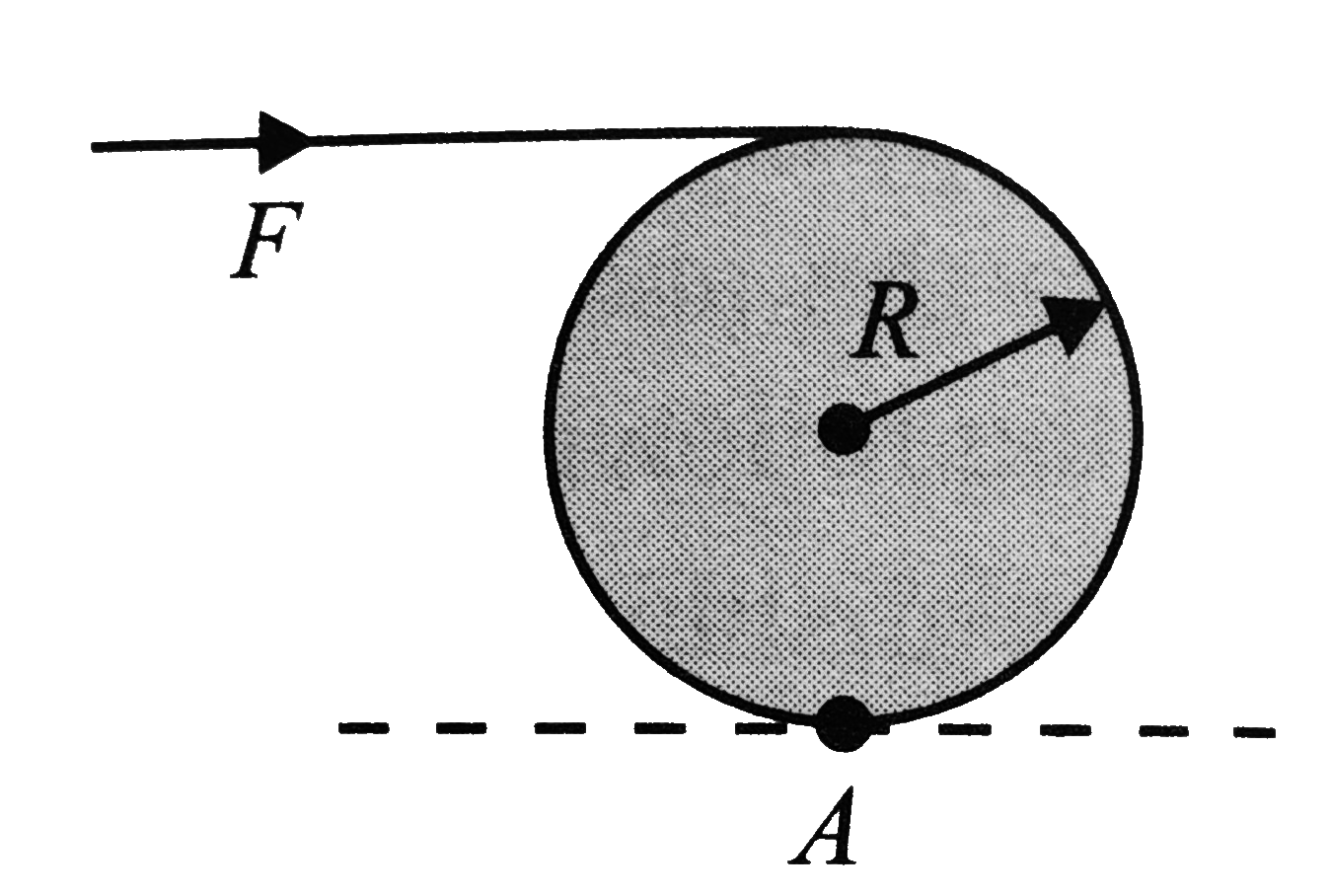
Tangential acceleration of the centre of mass isA3F4mBFmC2F3mD4F3m
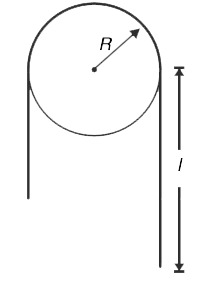
A rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
View SolutionA metallic pulley is in the shape of a disc of radius a. It can rotate freely about a horizontal axis passing through its centre. The moment of inertia of the pulley about this axis is I. A light string is tightly wrapped around the pulley with its one end connected to a block of mass M. The centre of the pulley and its circumference are connected to a resistance R as shown. The contact of resistance at the circumference does not cause any friction. A uniform magnetic field B is switched on which is parallel to the axis of rotation of the pulley (see Figure). The mass M is allowed to fall. Assume that resistivity of the material of the pulley is negligible.
(a) Find the acceleration of the block of mass M at the instant its velocity becomes v0.
(b) Assuming that the block can fall through a large distance, calculate the terminal speed (vT) that it will acquire.
(c) Find the rate of change of kinetic energy of the pulley at the instant speed of the falling block is vT2.

View SolutionA horizontally oriented uniform disc of mass M and radius R rotates freely about a stationary vertical axis passing through its centre. The disc has a radial guide along which can slide without friction a small body of mass m. A light thread running down through the hollow axle of the disc is tied to the body initially the body was located at the edge of the disc and the whole system rotated with ann angular velocity ω0. Then by means of a force F applied to the lower and of the thread the body was slowly pulled to the rotation axis. find:
(a). The angular velocity of the system in its final state.
(b). The work performed by the force F.
View SolutionA uniform disc of radius R and mass M is free to rotate about a fixed horizontal axis perpendicular to its plane and passing through its centre. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The block is released from rest. If string does not slip on the rim then find the acceleration of the block. Neglect the mass of the string.
View SolutionA cord with negligible mass is wrapped around a pulley that is a uniform disk of mass 5.00 kg and radius 0.300 m and that can rotate without friction about its central axis. A 1.0 kg bucket is attached at the free end of the cord hanging down from the pulley and then released at time t = 0. The cord begins to unwrap from the pulley as the bucket descends. At t = 5.00 s, through how many rotations has the pulley turned (the bucket is still descending)?
View SolutionA horizontal smooth rod AB rotates with a constant angular velocity ω=2.00rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m=0.50g moves along the rod from the point A with the initial velocity v0=1.00m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to rotating rod) at the moment when the sleeve is located at the distance r=50cm from the rotation axis.
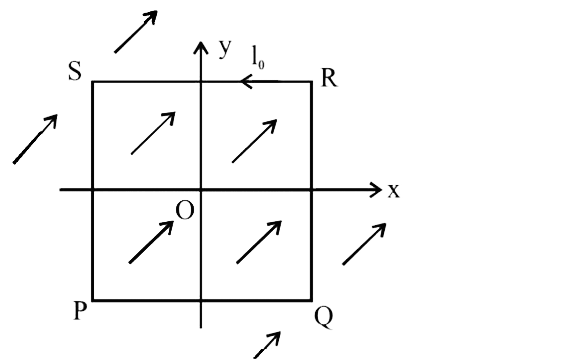
View SolutionA uniform constant magnetic field B is directed at an angle of 45∘ to the xaξs in the xy- plane . PQRS is a rigid, square wire frame carrying a steady current I0, with its centre at the origin O. At time t=0, the frame is at rest in the position as shown in figure , with its sides parallel to the xandy axis. Each side of the frame is of mass M and length L.
(a) What is the torque τ about O acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time Δt, and the axis about this rotation occurs .(Δtissoshorttˆanyvariation∈the→rquedur∈gthis∫ervalmaybe¬≤cted.)Given:themomentof∫eriaoftheameaboutanaξsthroughitscentreperpendica––r→itsaboutanaξsthroughitscentreperpendica––r→itspla≠is(4)/(3) ML^(2).
View Solution
