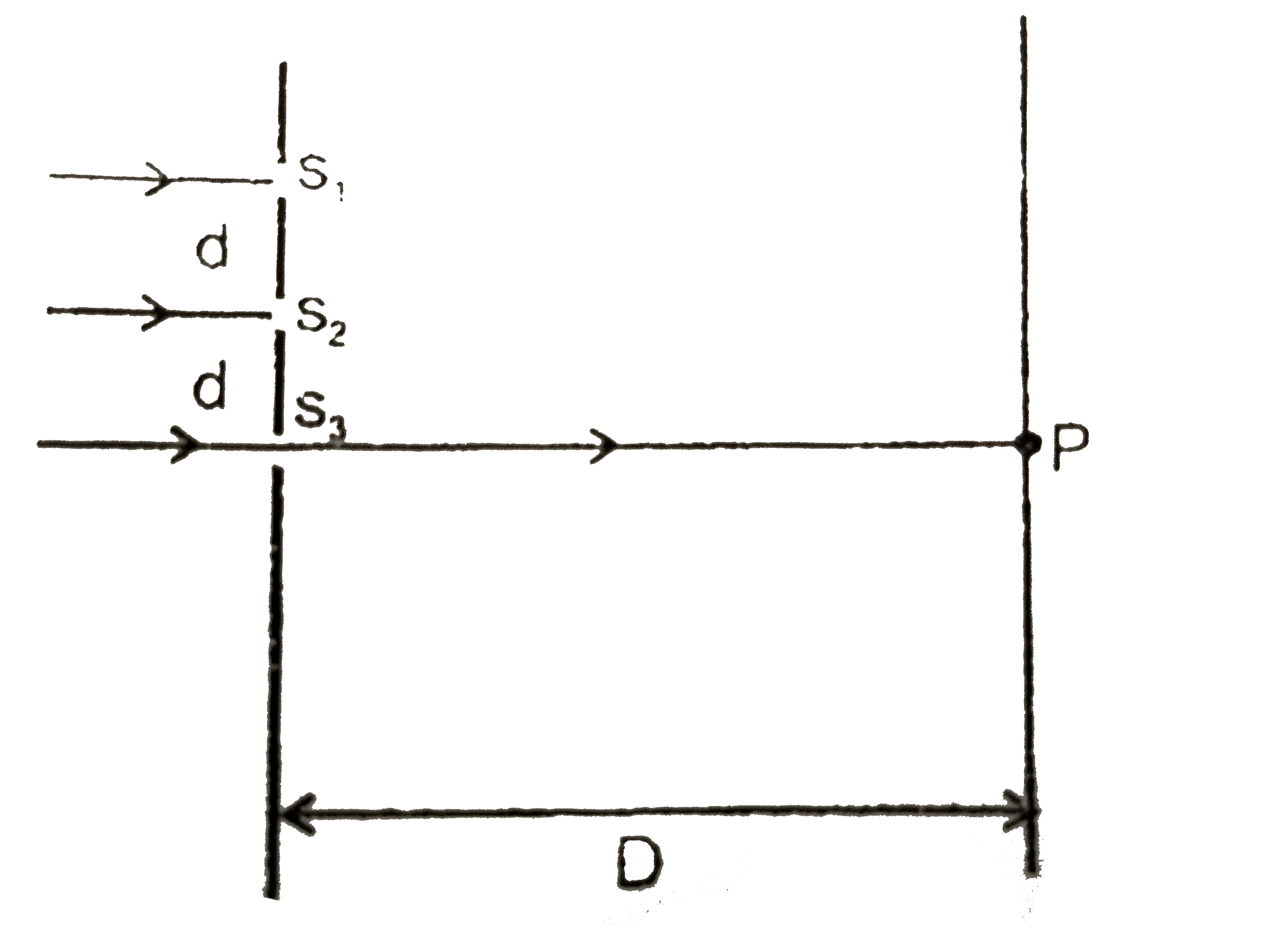
figure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let and .
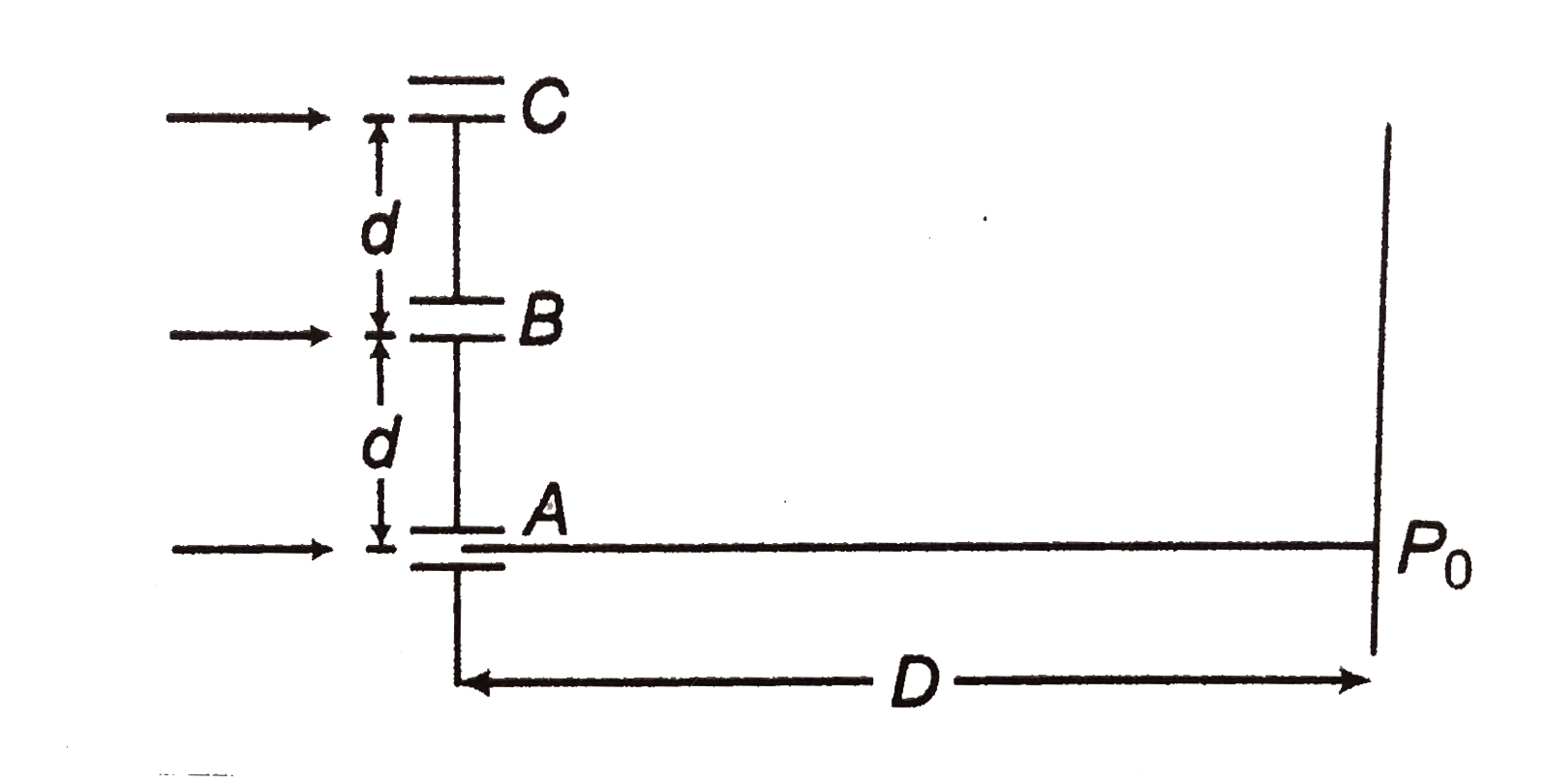
(a) Show that d =
(b) Show that the intensity at is three times the intensity due to any of the three slits
individually.
The correct Answer is:A
a.
(neglecting the term as it is very small)
b. To fing the inensity at P we have to consider the inteference of light waves coming from all the three slits.
So, the corresponding phase difference between waves from C and A is
..............i
.......i
so it can be said that light from B and C are i same phase as they have same phase difference with respect to A.
So,
[using vector method]
As the resulting amplitude is m3 times the intensity due to individual slits.
Topper's Solved these Questions
Similar Questions
Three narrow slits A, B and C are illuminated by a parallel beam of light of wavelengthλ , P is a point on the screen exactly in front of point A. Slit plane is at a distance D from the screen(D>>λ). It is know that BP – AP =13
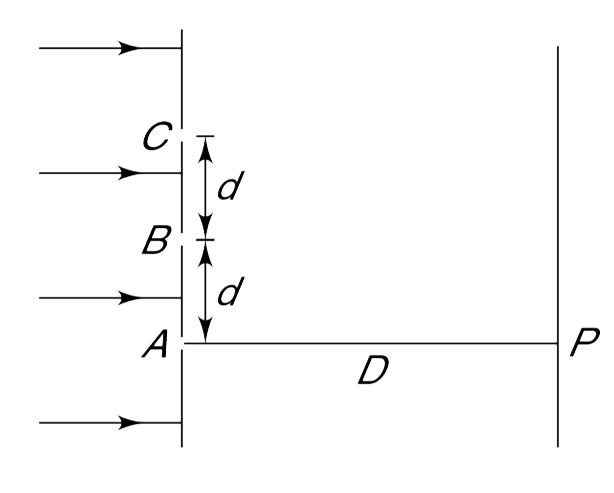
(a) Find d in terms of D andλ
(b) Write the phase difference between waves reaching at P from C and A.
(c) If intensity of P due to any of the three slits individu- ally is I0, find the resultant intensity at P.
View SolutionFigure shows a narrow slit S illuminated b a monochromatic light of wavelength λ in a double-slit experiment. In the path of the rays reaching the upper slit S1, a tube to length L is interposed in which the index of reflection of the medium varies linearly as shown in figure . The position of the central maximum in the interference pattern on the screen was displaceed by N fringes. Find the value of N in terms of μ0, L and λ.
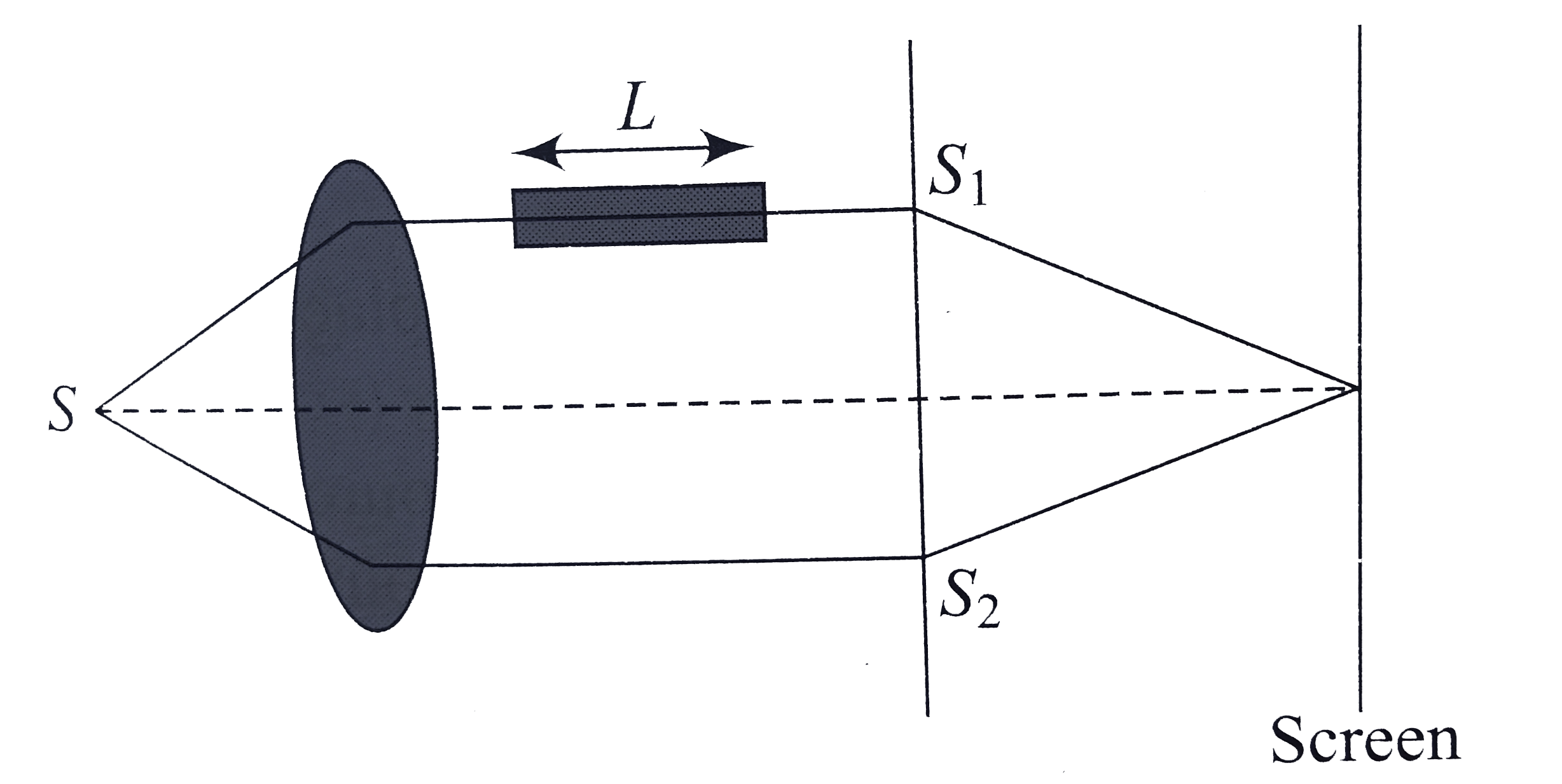
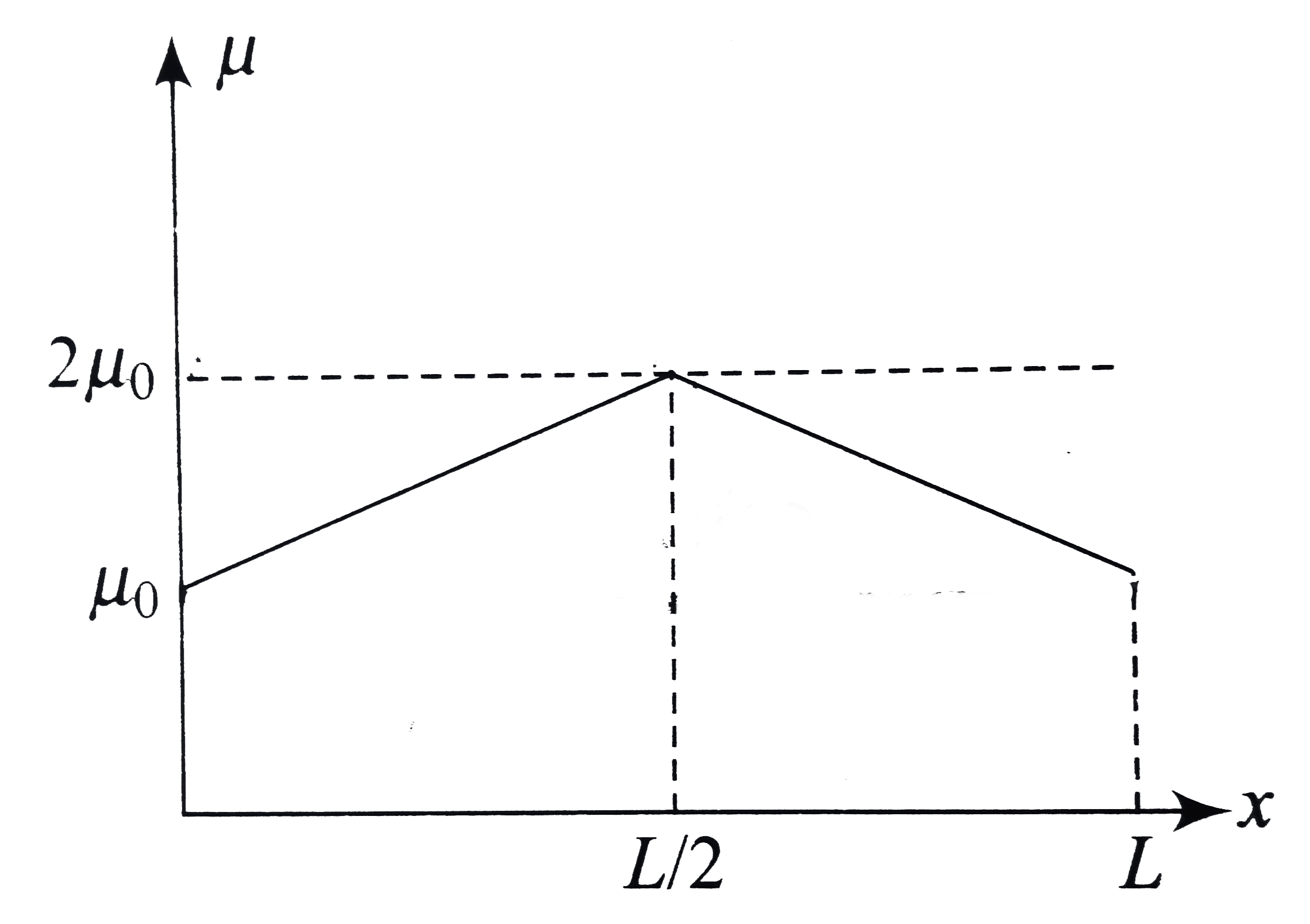
View Solution
Knowledge Check
_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-A3IB5IC8IDzero
Consider the situation shown in figure-6.35. The two slits S1 and S2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen E1 placed at a distance D from the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3. Another screen E2 is placed a further distance D away from E1. Find the ratio of the maximum to minimum intensity observed on E2 if z is equal is : (a)λD2d (b)λDd (c)λD4d

View SolutionA Young's double slit experiment uses a monochromatic light of wavelength λ. The intensity of each slit is same and is equal to I0. What will be the resultant intensity at a point where waves interfere at a path difference of λ2 ?
View SolutionIn the figure shown three slits s1,s2 and s3 are illuminated with of wavelength λ.λ<<d and D>>d. Each slit prouduces same intensity I on the screen. If intensity at the point on screen directly infront of s2 is 3I then the maximum value of λ is nd22D Find value of n.
View SolutionIn a Young's double slit set up using monochromatic light of wavelength λ the intensity of light at a point, where path difference is 2λ is found to be I0 What will be the intensity at a point when path different is λ/3 ?
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d

View SolutionThere are three forces F1,F2 and F3 acting on a body , all acting on a point P on the body . The body is found to move with uniform speed.
(a) Show that the forces are coplanar.
(b) Show that the torque acting on the body about any point due to these three forces is zero.
View SolutionThere are three forces F1,F2 and F3 acting on a body , all acting on a point P on the body The body is found to moves with unifrom speed (a) Show that the forces are coplaner.
(b) Show that the torque acting on the body about any point due to these three forces is zero .
View Solution
