Two coherent point sources S1andS2 emit light of wavelength λ. The separation between sources is 2λ. Consider a line passing through S2 and perpendicular to the line S1S2. What is the smallest distance on this line from S2 where a minimum of intensity occurs?
The correct Answer is:A, B, D
For minimum intensity
∴S1P−S2P=x=(2+1)λ2
Thus we get
→√Z2+(2λ)2−z=(2n+1)λ2
→Z2+4λ2(2n+1)2λ24
+2Z(2n+1)λ2
→Z=4λ2−(2n+1)2λ24(2n+1)λ
=16λ2−(2n+1)2λ24(2n+1)λ......i
Pu∈gn=0rarr z=(15lamda)/4<br>n=-1rarr z=(-15lamda)/4<br>n=1rarr z=(7lamda)/12<br>n=2rarrZ=(-9lamda)/20<br>:. Z=(7lamda)/12 is the smallest distnce for which there will be minimum intensity.
Topper's Solved these Questions
Similar Questions
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View SolutionTwo coherent point sources S1andS2 vibrating in phase emit light of wavelength λ . The separation between them is 2λ . The light is collected on a screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to the intensity at O
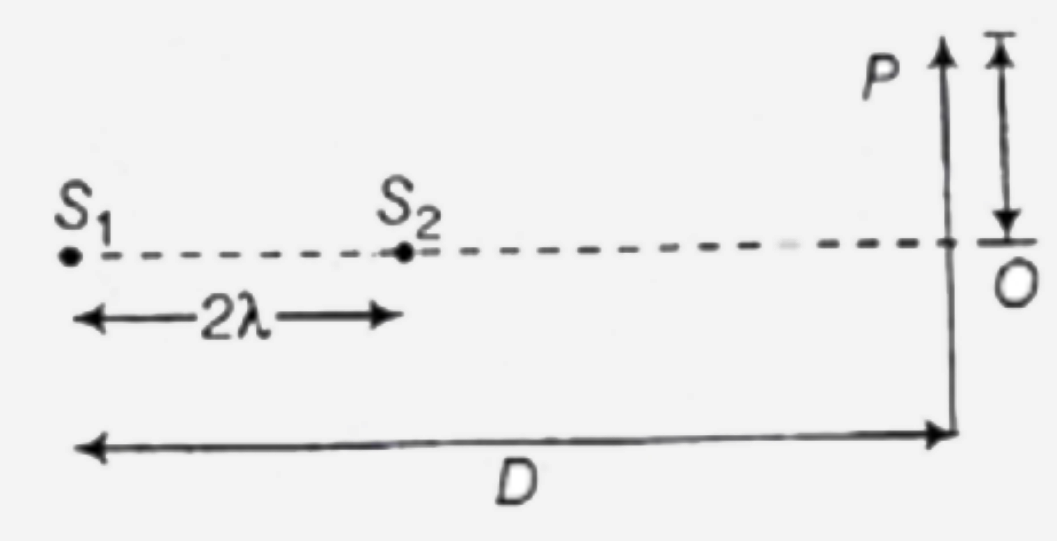
View Solution
Knowledge Check
Two coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S2 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .A7λ12B15λ4Cλ2D3λ4
.A7λ12B15λ4Cλ2D3λ4Two identical light sources S1 and S2 emit light of same wavelength λ. These light rays will exhibit interference if
A(a) Their phase differences remain constantB(b) Their phases are distributed randomlyC(c) Their light intensities remain constantD(d) Their light intensities change randomlyChoose the most appropriate option.
Two coherent point sources S1andS2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ. The light is collected ona screen placed at a distance D>>λ from the slit S1 as shown. The minimum distance, so that intensity at P is equal to intensity at O.
 A√2DB√3DC√8DD√5D
A√2DB√3DC√8DD√5D
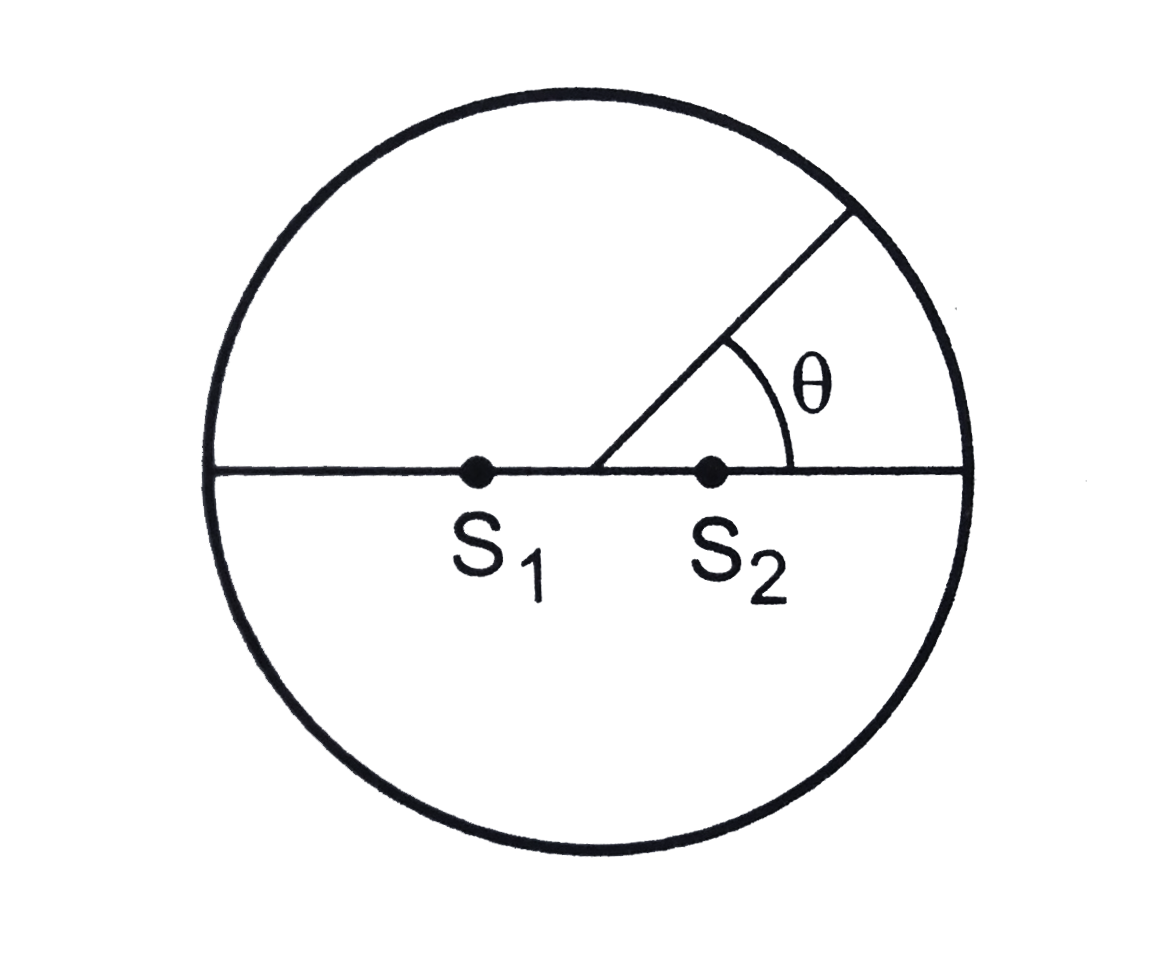
Figure shows two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2 is at the centre of the wire. Find the angular positions θ, on the wire for which constructive interference takes place.

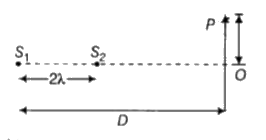
View SolutionTwo coherent point source S1 and S2 vibrating in phase emit light of wavelength λ. The separation between them is 2λ as shown in figure. The first bright fringe is formed at 'P' due to interference on a screen placed at distance 'D' from S1(D>>λ), then OP is

1) √3D,2)1.5D,3)√2D,4)2D
View SolutionThe two coherent sources of monochromatic light of wavelength λ are located at a separation λ. The two sources are placed on a horizontal line and screen is placed perpendicular to the line joining the sources. Find position of the farthest minima from the centre of the sources.
View SolutionFigure shows two coherent sources S1andS2which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire at large radius is placed in such a way that S1S2 lies in its plane and the middle point of S1S2, is at the centre of the wire. Find the angular positions 0 on the wire for which constructive interference takes place.
View SolutionTwo coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be

View Solution
