If A and B represent the complex numbers z1 and z2 such that |z1+z2|=|z1−z2|, then the circumcenter of △OAB, where O is the origin, is

A

z1+z23

B

z1+z22

C

z1−z22

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

We have,
|z1+z2|=|z1−z2|
⇒|z1+z2|2=|z1−z2|2
⇒4|z1||z2|2=|z1−z2|2
(wher θ1=arg(z1) and θ2=arg(z2]
⇒θ2−θ1=π2⇒∠AOB=π2
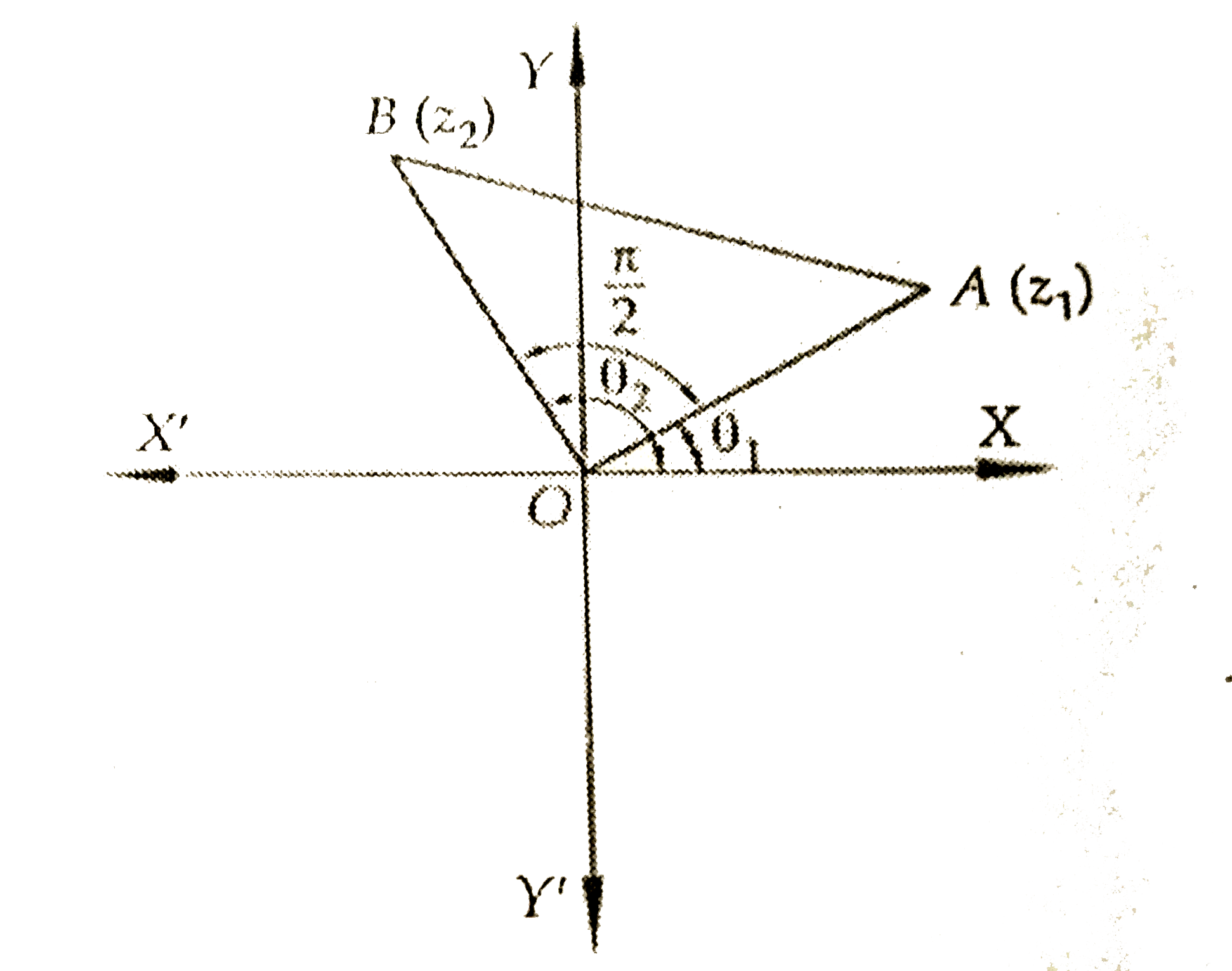
ocr_image
So, the circumcenter of △AOB is the mid-point of hypotenuse AB and its affix is z1+z22.

Updated on:21/07/2023
|
Class 12MATHSCOMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If P andn Q are represented by the complex numbers z1 and z2 such that |1/z2+1/z1|=|1/z2−1/z1|, then

    AΔOPQ (where O is the origin) is equilateral.
    BΔOPQ is right angled
    Cthe circumcentre of ΔOPQ is 12(z1+z2)
    Dthe circumcentre of ΔOPQ is 12(z1−z2)

  • If PandQ are represented by the complex numbers z1andz2 such that ∣∣∣1z2+1z1∣∣∣=∣∣∣1z2−1z1∣∣∣, then the circumstance of ΔOPQ (where O is the origin) is

    A12(z1−z2)
    B13(z1+z2)
    C12(z1+z2)
    D13(z1−z2)

  • For two complex numbersz1andz2 , we have ∣∣∣z1−z21−¯z1z2∣∣∣=1, then

    Aboth z1andz2 lie on circle |z|=1
    Barg(z1z2)=π3
    CAt least one of z1andz2 lies on the circle |z|=1
    D|z1|=2|z2|