A 200 mH (pure) inductor, and a 5μF (pure) capacitor , are connected , one by across a sinusoidal ac voltage source V=[70.7sin(1000t)] voltage. Obtain the expressions for the current in each case.
To solve the problem, we need to find the expressions for the current through a 200 mH inductor and a 5 µF capacitor when connected to an AC voltage source given by V(t)=70.7sin(1000t).
Step 1: Identify the given values
- Inductance, L=200mH=200×10−3H
- Capacitance, C=5μF=5×10−6F
- Voltage source, V(t)=70.7sin(1000t)
- Angular frequency, ω=1000rad/s
Step 2: Calculate the inductive reactance (XL)
The inductive reactance is given by the formula:
XL=ωL
Substituting the values:
XL=1000×(200×10−3)=200Ω
Step 3: Calculate the capacitive reactance (XC)
The capacitive reactance is given by the formula:
XC=1ωC
Substituting the values:
XC=11000×(5×10−6)=10.005=200Ω
Step 4: Calculate the amplitude of the current for the inductor
Using Ohm's law for AC circuits, the amplitude of the current (I0) through the inductor is given by:
I0=V0XL
Where V0=70.7. Thus:
I0=70.7200=0.3535A
Step 5: Write the expression for the current through the inductor
The current through the inductor lags the voltage by 90 degrees:
IL(t)=I0sin(1000t−π2)=0.3535sin(1000t−90∘)
Step 6: Calculate the amplitude of the current for the capacitor
Using the same formula for the capacitor:
I0=V0XC
Since XC=200Ω, we have:
I0=70.7200=0.3535A
Step 7: Write the expression for the current through the capacitor
The current through the capacitor leads the voltage by 90 degrees:
IC(t)=I0sin(1000t+π2)=0.3535sin(1000t+90∘)
Final Expressions
1. Current through the inductor:
IL(t)=0.3535sin(1000t−90∘)
2. Current through the capacitor:
IC(t)=0.3535sin(1000t+90∘)
- Inductance, L=200mH=200×10−3H
- Capacitance, C=5μF=5×10−6F
- Voltage source, V(t)=70.7sin(1000t)
- Angular frequency, ω=1000rad/s
The inductive reactance is given by the formula:
XL=ωL
Substituting the values:
XL=1000×(200×10−3)=200Ω
The capacitive reactance is given by the formula:
XC=1ωC
Substituting the values:
XC=11000×(5×10−6)=10.005=200Ω
Using Ohm's law for AC circuits, the amplitude of the current (I0) through the inductor is given by:
I0=V0XL
Where V0=70.7. Thus:
I0=70.7200=0.3535A
The current through the inductor lags the voltage by 90 degrees:
IL(t)=I0sin(1000t−π2)=0.3535sin(1000t−90∘)
Using the same formula for the capacitor:
I0=V0XC
Since XC=200Ω, we have:
I0=70.7200=0.3535A
The current through the capacitor leads the voltage by 90 degrees:
IC(t)=I0sin(1000t+π2)=0.3535sin(1000t+90∘)
1. Current through the inductor:
IL(t)=0.3535sin(1000t−90∘)
2. Current through the capacitor:
IC(t)=0.3535sin(1000t+90∘)
Topper's Solved these Questions
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - C.B.S.E.CLASS-XII PHYSICS (THEORY) [SET-I] (SECTION-A)
5 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTIONS-B
4 Videos
- XII BOARDSBOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - XII BOARDSEXERCISE - SECTION-C
50 Videos
- SAMPLE PAPER 2019BOOK - XII BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION D
6 Videos
Similar Questions
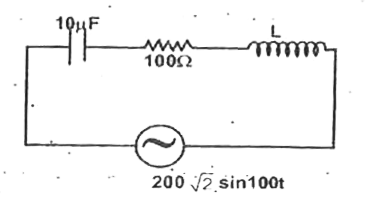
A 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
View SolutionA satellite is launched into a circular orbit of radius R around the earth while a second satellite is launched into an orbit of radius 1.02R. The percentage difference in the time period is:
View SolutionA 400 Ω resistor, a 3 H inductor and a 5 μF capacitor are connected in series to a 220 V, 50 Hz ac source. Calculate the :
(1) Impedance of the ciruit.
(ii) Current flowing through the circuit.
View SolutionA circuit containing an 80mH inductor and a 60μF capacitor in series is connected to a 230V−50Hz Supply. The resistance in the circuit is negligible .
(a) Obtain the current amplitude and rms currents.
(b) Obtain the rms values of voltage across inductor and capacitor.
(c ) What is the average power transferred to the inductor and to the capacitor?
(d) What is the total power absorbed by the circuit?
View SolutionA 9/100(π) inductor and a 12Ω resistanace are connected in series to a 225 V, 50 Hz ac source. Calculate the current in the circuit and the phase angle between the current and the source voltage.
View SolutionA 1.00mH inductor and a 1.00μF capacitor are connected in series. The current in the circuit is described by i=20t, where t, is in second and i is in ampere. The capacitor initially has no charge. Determine
(a) the voltage across the inductor as a function of time,
(b) the voltage across the capacitor as a function of time,
(c) the time when the energy stored in the capacitor first exceeds that in the inductor.
View SolutionA 200Ω resistor is connected in series with a 5(μ)F capacitor. The voltage across the resistor is VR=(1.20V)cos(2500rads−1)t.
(a) Derive an expression for the circuit current.
(b) Determine the capacitive reactance of the capacitor.
View SolutionA 4.00μF capacitor and a 6.00μF capacitor are connected in parallel across a 660V supply line
(a) Find the charge on each capacitor and the voltage across each.
(b) The charged capacitors are disconnected from the line and from each other, and reconnected to each other with terminals of unlike sign together. Find the final charge on each and the voltage across each.
View SolutionAn inductor (L=2000mH) is connected to an AC source of peak current. What is the instantaneous voltage of the source when the current is at its peak value?
View SolutionA capacitor of capacitance 10μF is connected to an AC source and an AC Ammeter. If the source voltage varies as V=50√2sin100t, the reading of the ammeter is
View Solution
