A bar of mass m and length l is hanging from point A as shown in figure.Find the increase in its length due to its own weight. The young's modulus of elasicity of the wire is Y and area of cross-section of the wire is A.
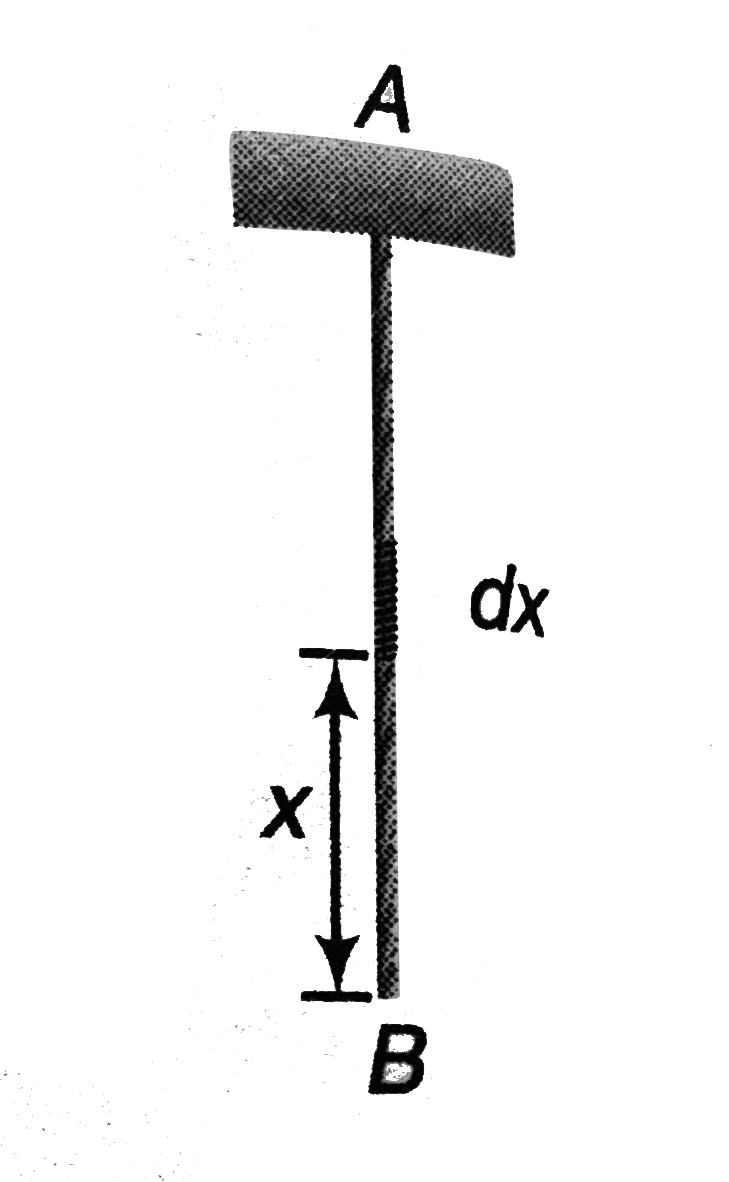
Consider a small section dx of the bar at a distance x from B. The weight of the bar for a length x is,
w=(mgl)x
Elongation in section dx will be, dl=(wAY)dx=(mglAY)xdx
Total elongation in the bar can be obtained by integrating this expression for x=0 to x=l.
∴ Δl=∫x=1x=0dl=(mglAY)∫10xdx
or Increase in length, Δl=mgl2AY
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.1
15 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Check point 12.2
15 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective
10 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
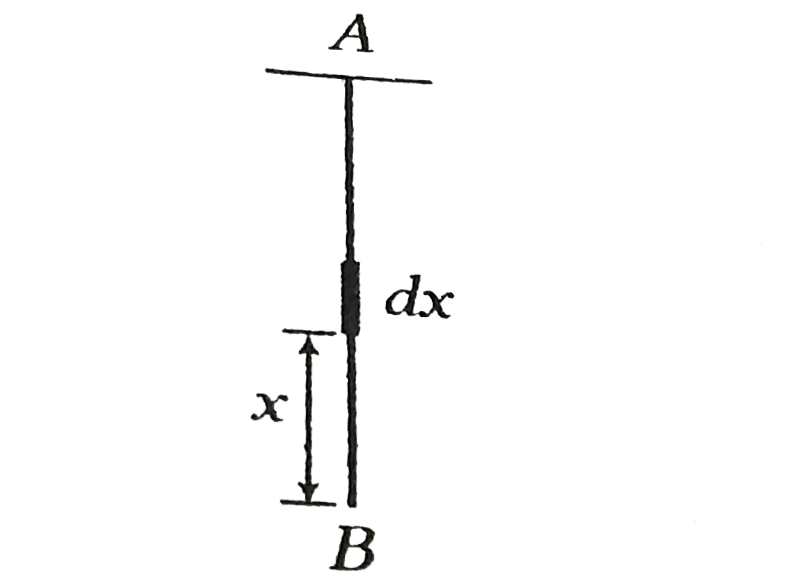
A bar of mass m and length l is hanging from point A as shown in the figure . If the Young's modulus of elasticity of the bar is Y and area of cross - section of the wire is A, then the increase in its length due to its own weight will be

View SolutionA bar of mass M and length L is hanging from point S as shown in figure. The Young's modulus of elasticity of the wire is Y and the area of cross-section of the wire is A.

(i) Find the stress at x distance from bottom end.
(ii) Consider a samll section dx of the bar at a distance x from lowest point of bar. Find elongation (dL) in section dx.
(iii) Find total elongation in bar.
(iv) Find energy density at x distance from bottom and.
(v) Find total elastic potential energy stored in bar.
View Solution
Knowledge Check
A thick rope of density ρ and length L is hung from a rigid support. The increase in length of the rope due to its own weight is (Y is the Young's modulus)
A0.14YρL2gB12YρL2gCρL2gYDρLgYA wire of mass m and length l is suspended from a ceiling. Due to its own wieght it elongates, consider cross-section are of wire as A ans Young's modulus of material of wire as Y. Th eelongation in the wire is
A2mg3YABmglYACmgl2YADcannot be calcuatedA wire suspended vertically from one of its ends is stretched by attaching a weight of 20 N to its lower end. If its length changes by 1% and if the Young's modulus of the material of the wire is 2×1011N/m2, then the area of cross section of the wire is
A1mm2B10−1mm2C10−2mm2D10−3mm2
Two blocks of masses m1 and m2 are hanging from a pulley with the help of a ropw of Young's modulus Y as shown in the diagram. The length of the wire is L and area of cross section is A. When system is released from rest, the elongation in the length of wire is.

View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View SolutionIf the length of a wire is doubled, then its Young's modulus
View SolutionA uniform wire of radius r and length L hanging vertically and fixed at its upper ends, is attached to a weight at its lower end. If Young's modulus for the material of the wire is Y, the extension is
View SolutionA wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the torce corstant of the wire is
View Solution
