Question

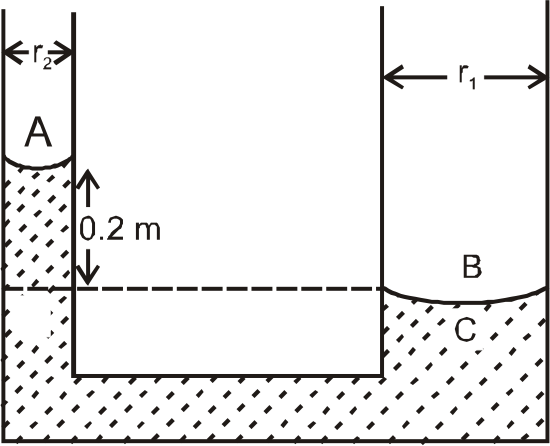
A barometer contains two uniform capillaries of radii $1.4\times {10}^{-3}m$ and $7.2\times {10}^{-4}m$. If the height of liquid in narrow tube is $0.2m$ more than that in wide tube, calculate the true pressure difference. Density of liquid $={10}^{3}kg/m^3$, surface tension $=72\times {10}^{-3}N/m$ and $g=9.8m{s}^{-12}$.

Answer

A::B

Explanation

To solve the problem, we need to calculate the true pressure difference between two capillaries based on the given parameters. Here’s a step-by-step breakdown of the solution:

Step 1: Identify Given Values
- Radii of the capillaries:
- \( R_1 = 1.4 \times 10^{-3} \, \text{m} \) (narrow tube)
- \( R_2 = 7.2 \times 10^{-4} \, \text{m} \) (wide tube)
- Height difference of liquid:
- \( H = 0.2 \, \text{m} \)
- Density of liquid:
- \( \rho = 10^3 \, \text{kg/m}^3 \)
- Surface tension:
- \( T = 72 \times 10^{-3} \, \text{N/m} \)
- Acceleration due to gravity:
- \( g = 9.8 \, \text{m/s}^2 \)

Step 2: Write the Pressure Difference Equation
The pressure difference \( \Delta P \) between the two points in the capillaries can be expressed as:
\( \Delta P = P_1 - P_2 = \rho g H + 2T \left( \frac{1}{R_1} - \frac{1}{R_2} \right) \)
Where:
- \( P_1 \) is the pressure in the narrow tube.
- \( P_2 \) is the pressure in the wide tube.

Step 3: Substitute the Known Values
Now, substituting the known values into the equation:
\( \Delta P = 10^3 \times 9.8 \times 0.2 + 2 \times 72 \times 10^{-3} \left( \frac{1}{1.4 \times 10^{-3}} - \frac{1}{7.2 \times 10^{-4}} \right) \)

Step 4: Calculate Each Component
1. Calculate the hydrostatic pressure difference:
\( \rho g H = 10^3 \times 9.8 \times 0.2 = 1960 \, \text{N/m}^2 \)

2. Calculate the surface tension contribution:
- First, calculate \( \frac{1}{R_1} \) and \( \frac{1}{R_2} \):
\( \frac{1}{R_1} = \frac{1}{1.4 \times 10^{-3}} \approx 714.29 \, \text{m}^{-1} \)
\( \frac{1}{R_2} = \frac{1}{7.2 \times 10^{-4}} \approx 1388.89 \, \text{m}^{-1} \)
- Now, find the difference:
\( \frac{1}{R_1} - \frac{1}{R_2} = 714.29 - 1388.89 = -674.60 \, \text{m}^{-1} \)
- Now calculate the surface tension term:
\( 2T \left( \frac{1}{R_1} - \frac{1}{R_2} \right) = 2 \times 72 \times 10^{-3} \times (-674.60) \approx -97.32 \, \text{N/m}^2 \)

Step 5: Combine the Results
Now, combine the hydrostatic pressure difference and the surface tension contribution:
\( \Delta P = 1960 - 97.32 \approx 1862.68 \, \text{N/m}^2 \)

Step 6: Final Result
Thus, the true pressure difference \( P_1 - P_2 \) is approximately:
\( \Delta P \approx 1860 \, \text{N/m}^2 \)