A battery charges a parallel plate capacitor of thickness (d) so that an energy [U0] is stored in the system. A slab of dielectric constant (K) and thickness (d) is then introduced between the plates of the capacitor. The new energy of the system is given by
KU0
K2U0
U0K
U0K2
The correct Answer is:A
To solve the problem step by step, we need to analyze the situation before and after the introduction of the dielectric slab in the parallel plate capacitor.
Step 1: Understand the Initial Conditions
Initially, we have a parallel plate capacitor with:
- Thickness = d
- Initial energy stored = U0
The energy stored in a capacitor is given by the formula:
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
Step 2: Determine the Initial Capacitance
The capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
where:
- ε0 is the permittivity of free space
- A is the area of the plates
- d is the separation between the plates
Step 3: Relate Initial Energy to Capacitance and Voltage
From the initial energy stored U0, we can express it as:
U0=12CV2
This can be rearranged to find CV2:
CV2=2U0
Step 4: Introduce the Dielectric Slab
When a dielectric slab with dielectric constant K and thickness d is introduced between the plates, the new capacitance C′ becomes:
C′=K⋅C
Step 5: Calculate the New Energy Stored
The new energy U′ stored in the capacitor after the dielectric is introduced can be expressed as:
U′=12C′V2
Substituting C′ into the equation:
U′=12(K⋅C)V2
Step 6: Substitute CV2 from Initial Conditions
Now, we can substitute CV2 from the earlier step:
U′=12(K⋅C)V2=K⋅12CV2=K⋅U0
Final Result
Thus, the new energy of the system after introducing the dielectric slab is:
U′=K⋅U0
Initially, we have a parallel plate capacitor with:
- Thickness = d
- Initial energy stored = U0
U=12CV2
where C is the capacitance and V is the voltage across the capacitor.
The capacitance C of a parallel plate capacitor is given by:
C=ε0Ad
where:
- ε0 is the permittivity of free space
- A is the area of the plates
- d is the separation between the plates
From the initial energy stored U0, we can express it as:
U0=12CV2
This can be rearranged to find CV2:
CV2=2U0
When a dielectric slab with dielectric constant K and thickness d is introduced between the plates, the new capacitance C′ becomes:
C′=K⋅C
The new energy U′ stored in the capacitor after the dielectric is introduced can be expressed as:
U′=12C′V2
Substituting C′ into the equation:
U′=12(K⋅C)V2
Now, we can substitute CV2 from the earlier step:
U′=12(K⋅C)V2=K⋅12CV2=K⋅U0
Thus, the new energy of the system after introducing the dielectric slab is:
U′=K⋅U0
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
Separation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View SolutionThe two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adjusted that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View SolutionTwo identical parallel plate capacitors are connected in series to a battery of 100V. A dielectric slab of dielectric constant 4.0 is inserted between the plates of second capacitor. The potential difference across the capacitors will now be respectively
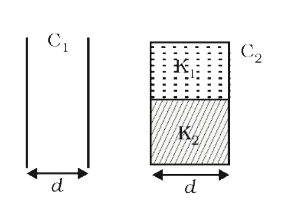
View SolutionYou are given an air filled parallel plate capacitor c1. The space between its plates is now filled with slabs of dielectric constant k1andk2 as shown in c2. Find the capacitances of the capacitor c2 if area of the plates is A distance between the plates is d.
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View Solution
