A battery is connected between two points A and B on the circumference of a uniform conducting ring of radius r and resistance R. One of the arc AB of the ring subtends an angle $θ$ at the centre. The value of the magnetic field produced at the centre due to the current in the ring is

A

proportional to $2 (180^{\circ} - θ)$

B

inversely proportional to r

C

zero, only if $θ = 180^{\circ}$

D

zero for all values $θ$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

(d) Magnetic field at the centre due to current in arc ACB is
$B_{1} = \frac{μ_{0}}{4 π} \frac{2 π I_{1}}{r} \frac{θ}{2 π}$ (directed upwards)
magnetic field at the centre due to current in arc ADB is
$B_{2} = \frac{μ_{0}}{4 π} \frac{2 π I_{2}}{r} \frac{2 π - θ}{2 π}$ (directed downwards)

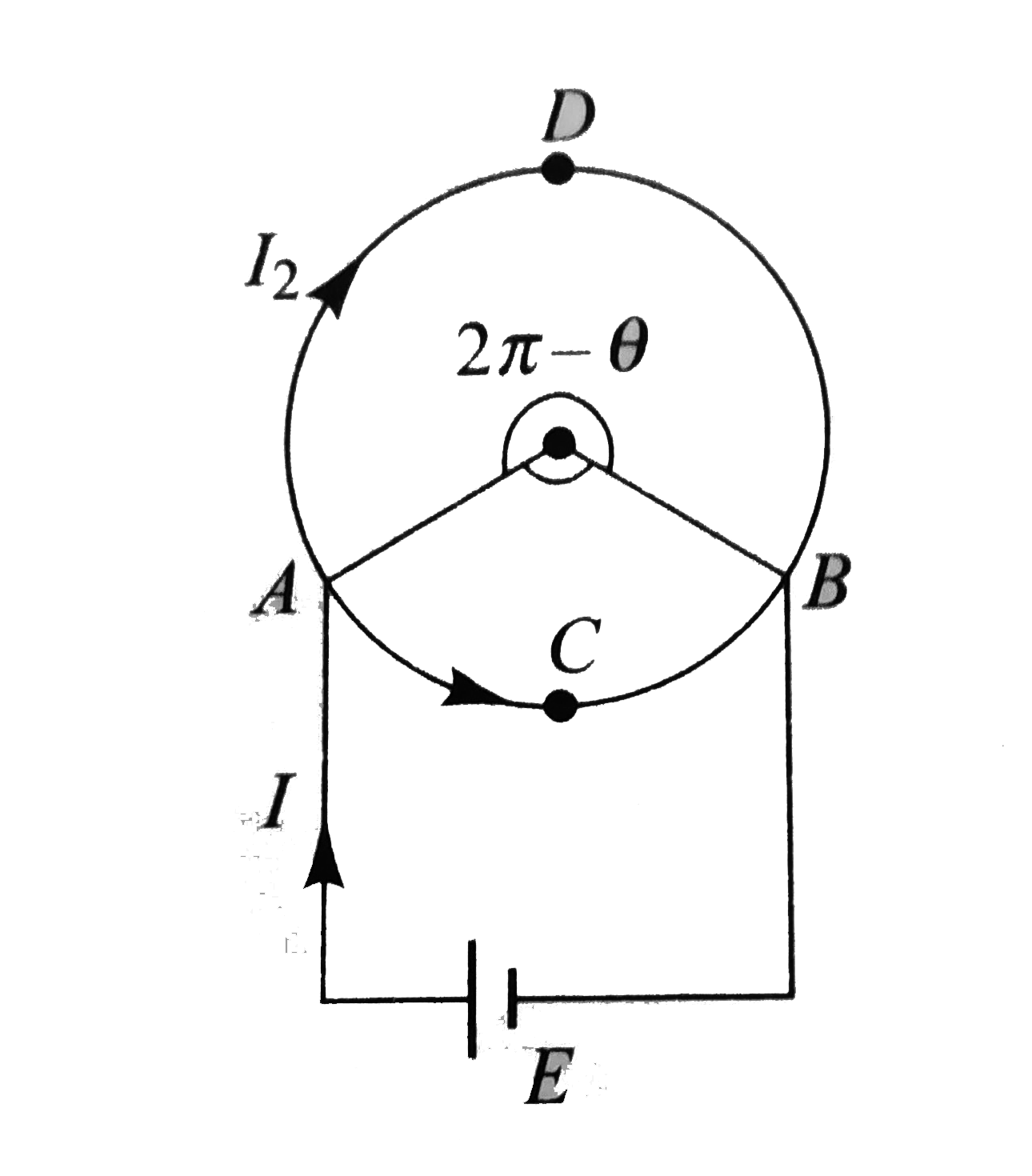
Therefore, net magnetic field at the centre
$B = \frac{μ_{0}}{4 π} \frac{2 π I_{1}}{r} \frac{θ}{2 π} - \frac{μ_{0}}{4 π} \frac{2 π I_{2}}{r} \frac{2 π - θ}{2 π}$
Also, $I_{1} = \frac{E}{R_{1}} = \frac{E}{ρ l_{1} / A} = \frac{E A}{ρ r θ}$
And $I_{2} = \frac{E}{R_{2}} = \frac{E}{ρ l_{2} / A} = \frac{E A}{ρ r (2 π - θ)}$
$∴ B = \frac{μ_{0}}{4 π} [\frac{E A}{ρ r θ} \times \frac{θ}{r} - \frac{E A}{ρ r (2 π - θ)} \times \frac{(2 π - θ)}{r}] = 0$
(d) is the correct option.

Updated on:21/07/2023

|

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-SOURCES OF MAGNETIC FIELD-Archives (single Correct Anser)

Home
Ask Doubt
Profile