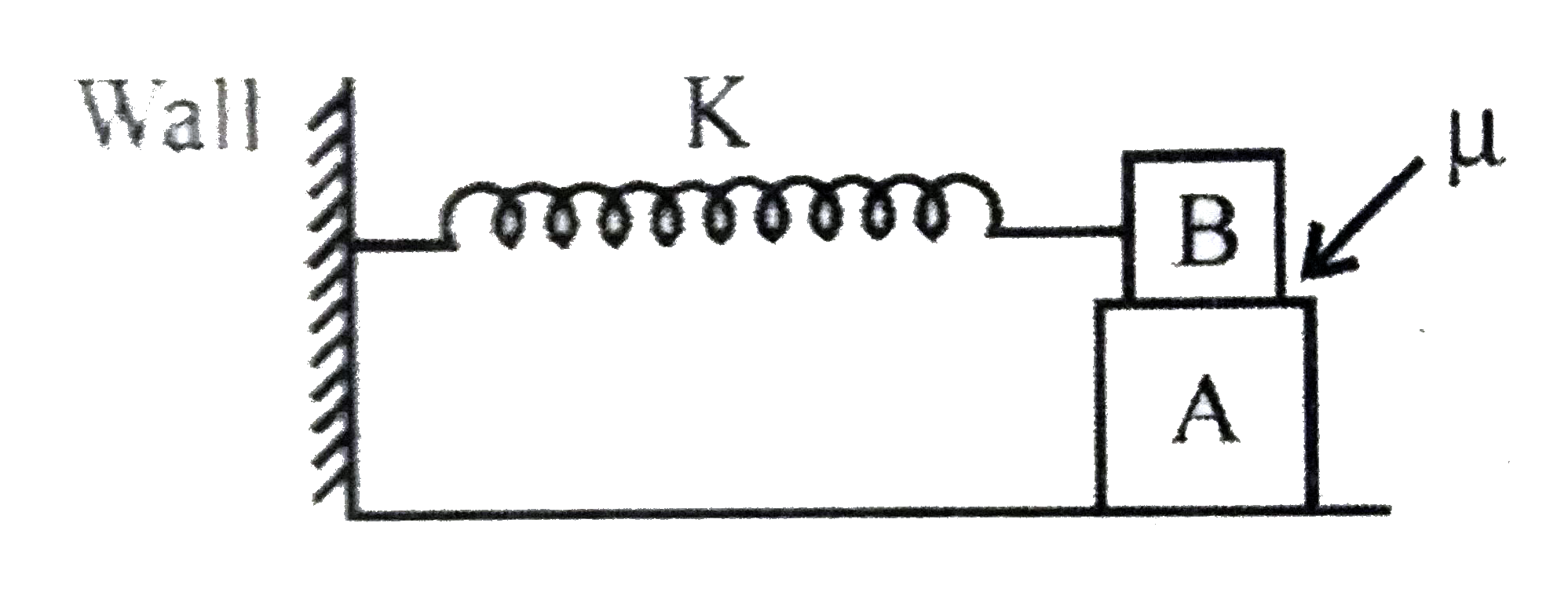
A block A of mass m is placed on a frictionless horizontal surface. Another block B of the same mass is kept on A and connected to the wall with the helpf of a spring of force constant K as shown in the figure. The coefficient of friction between the blocks A and B is μ. The blocks move together execting simple harmonic motion of amplitude 'a'. What is the maximum value of the fricitional force between A and B ?
μ mg
zero
Ka
Ka2
The correct Answer is:D
Because of the compressions and extensions of the spring, A and B move together executing a linear S.H.M. The maximum acceleration of the system =ω2 a where a is the amplitude. A and B are not rigidly fixed. Hence there is a tendency for relative motion between them. There will be no relative motion between A and B or they will move together, as long as the limiting force of friction (f) between them =mass of B × maximum acceleration
i.e. f=mω2a where ω=√Km+m=√K2m
∴f=m.K2m×a=Ka2
Topper's Solved these Questions
Similar Questions
A block of mass m =1 kg placed on top of another block of mass M = 5 kg is attached to a horizontal spring of force constant K = 20 N/m as shown in figure. The coefficient of friction between the blocks is µ where as the lower block slides on a frictionless surface. The amplitude of oscillation is 0.4 m. What is the minimum value of µ such that the upper block does not slip over the lower block ?

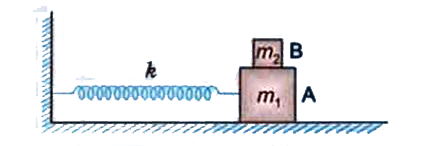
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
View Solution
Knowledge Check
A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
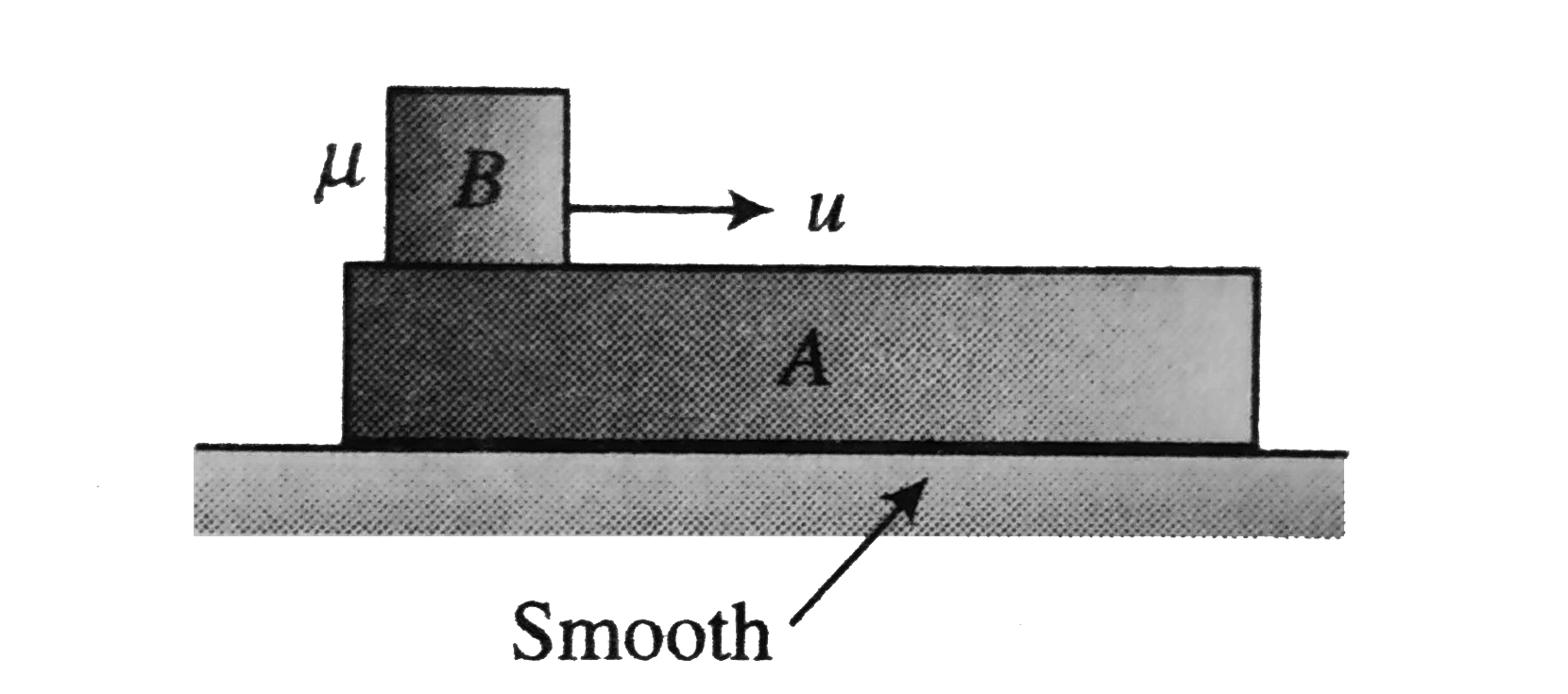 A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.Two block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
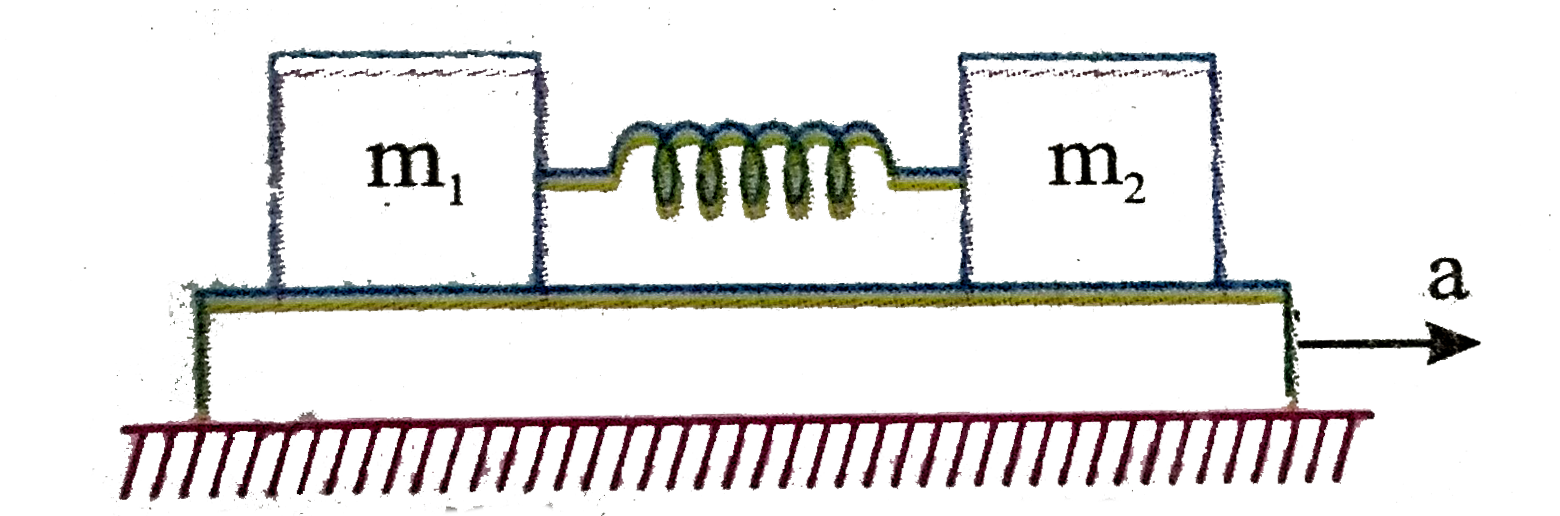 Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.
Aspring will be stretched if a>μgBspring will be commpressed if a≤μgCspring will neither be compressed nor be stretched for a<μg only.Dspring will be in its natural length under all conditions.A block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
 A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A−μmgk+1k√(μmg)2+mkv2Bμmgk+1k√(μmg)2+mkv2C−μmgk+1k√(μmg)2−mkv2Dμmgk+1k√(μmg)2+mkv2
A block of mass m1 resting on a frictionless horizontal surface is connected to a spring of spring constant k that is anchored in a near by wall. A block of mass m2 is placed on the top of the first block. The coefficient of static friction between the two blocks is μ Assuming that the two blocks move together as a unit, find the period of oscillation of the system and also find maximum oscillation amplitude that permits the two bodies to move as a unit.
View SolutionA block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
View SolutionA block P of mass m is placed on a smooth horizontal surface. A block Q of the same mass is placed over the block P and the coefficient of static friction between them is μ. A spring of spring constant K is attached to block Q. The blocks are displaced together to a distance A and released. The upper block oscillates without slipping over the lower block. The maximum frictional force between the block is:
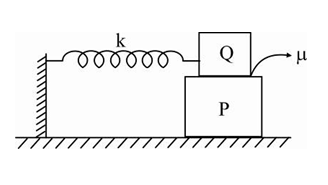
View SolutionThere block A B ,and C of equal mass m are placed one over the other on a frictionless surface (table) as shown in figure The coefficient of friction between any blocks A ,B and C is μ The maximum value of mass of block D so that the blocks A,B and C move without slipping over each other is
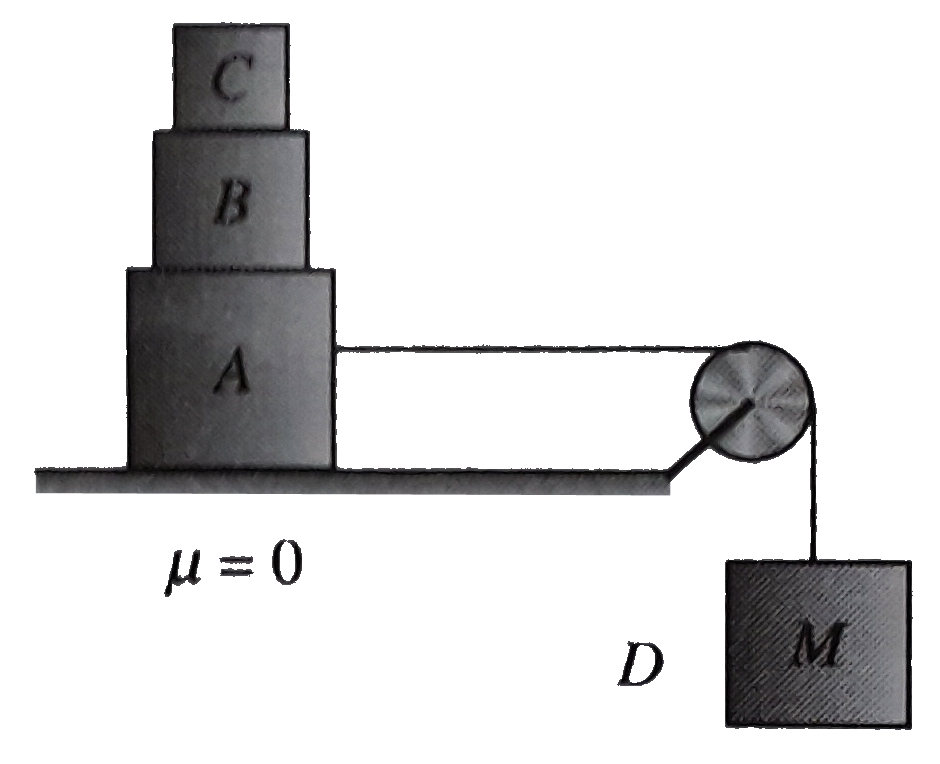
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View Solution
