A block of mass is placed on a surface with a vertical cross section given by y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is:
(a) 16m
(b) 23m
(c) 13m
(d) 12m
The correct Answer is:A
To solve the problem, we need to determine the maximum height at which a block can be placed on a surface described by the equation y=x36 without slipping, given that the coefficient of friction is μ=0.5.
1. Understand the Surface Equation:
The surface is defined by the equation:
y=x36
This represents a curve in the xy-plane.
2. Find the Slope of the Surface:
To find the slope of the surface at any point, we differentiate y with respect to x:
dydx=ddx(x36)=3x26=x22
3. Relate the Slope to the Coefficient of Friction:
The maximum angle of inclination before slipping occurs can be determined using the coefficient of friction. The condition for slipping is given by:
tan(θ)=μ
where θ is the angle of the slope. For small angles, we can approximate tan(θ) by the slope:
dydx=μ
Substituting the values we have:
x22=0.5
4. Solve for x:
Rearranging the equation gives:
x2=0.5×2=1
Taking the square root:
x=±1
We will consider x=1 since we are looking for the maximum height.
5. Calculate the Maximum Height y:
Now, substitute x=1 back into the equation for y:
y=(1)36=16
6. Final Result:
The maximum height above the ground at which the block can be placed without slipping is:
16
The surface is defined by the equation:
y=x36
This represents a curve in the xy-plane.
To find the slope of the surface at any point, we differentiate y with respect to x:
dydx=ddx(x36)=3x26=x22
The maximum angle of inclination before slipping occurs can be determined using the coefficient of friction. The condition for slipping is given by:
tan(θ)=μ
where θ is the angle of the slope. For small angles, we can approximate tan(θ) by the slope:
dydx=μ
Substituting the values we have:
x22=0.5
Rearranging the equation gives:
x2=0.5×2=1
Taking the square root:
x=±1
We will consider x=1 since we are looking for the maximum height.
Now, substitute x=1 back into the equation for y:
y=(1)36=16
The maximum height above the ground at which the block can be placed without slipping is:
16
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
Similar Questions
A block of mass 'm' is placed on a rough surface with a vertical cross section of y=x36. If the coefficient of friction is 0.5, the maximum height above the ground at which the block can be placed without slipping is .
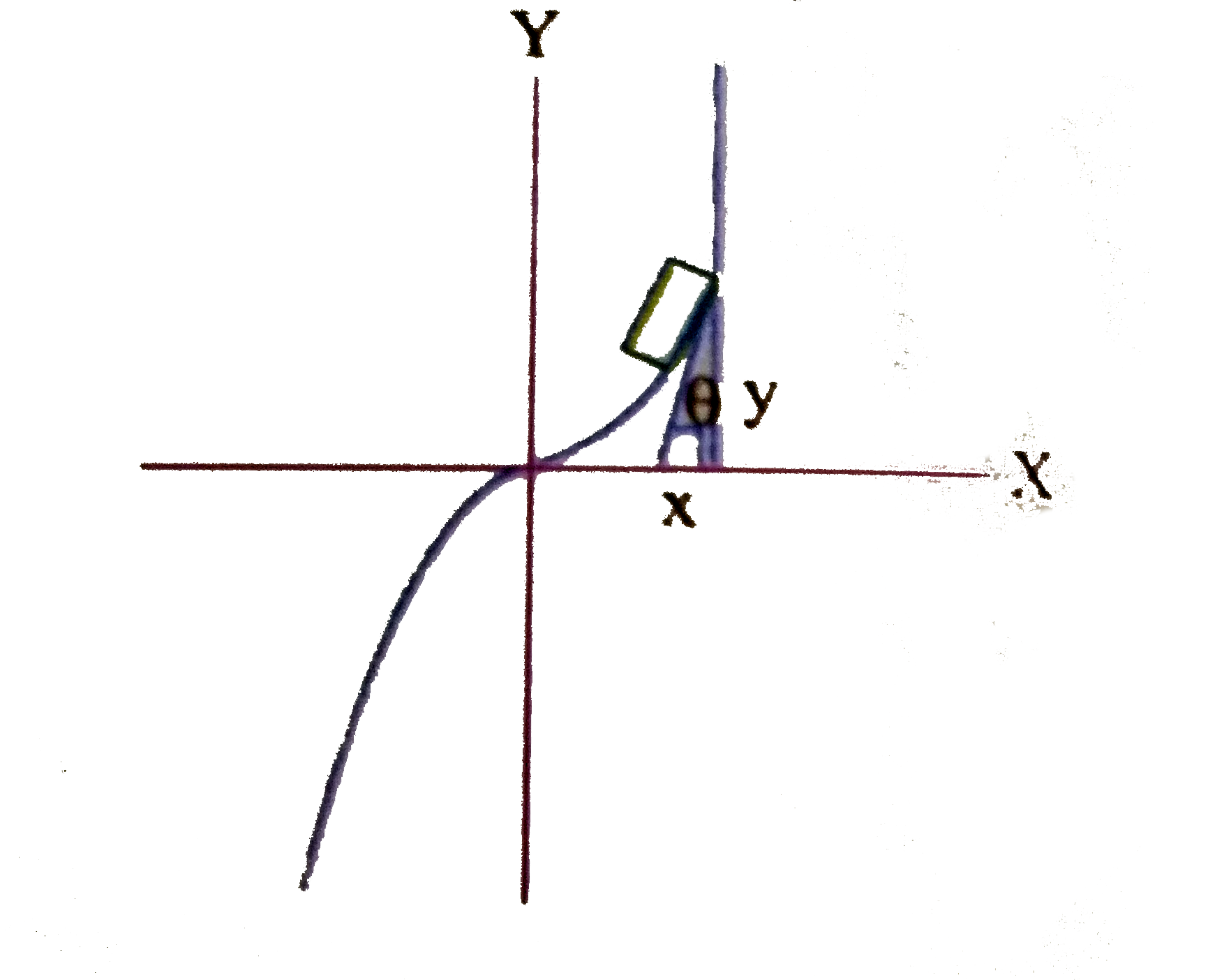
View SolutionA block of mass m is palced on a surface having coefficient of frictionn 0.25, with a vertical cross section given by y=x416. Calculate the maximum height above the ground t which block can be placed without slipping.
View Solution
Knowledge Check
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it isAμgBμMmgCμmMgDgμA block of mass 1 kg is held at rest against a rough vertical surface by pushing by a force F horizontally. The coefficient of friction is 0.5. When
 AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.
AF = 40 N, friction on the block is 20 N.BF = 30 N, friction on the block is 10 N.CC = 20 N, friction on the block is 10 N.DMinimum value of force F to keep block at rest is 20 N.A block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNone
A block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
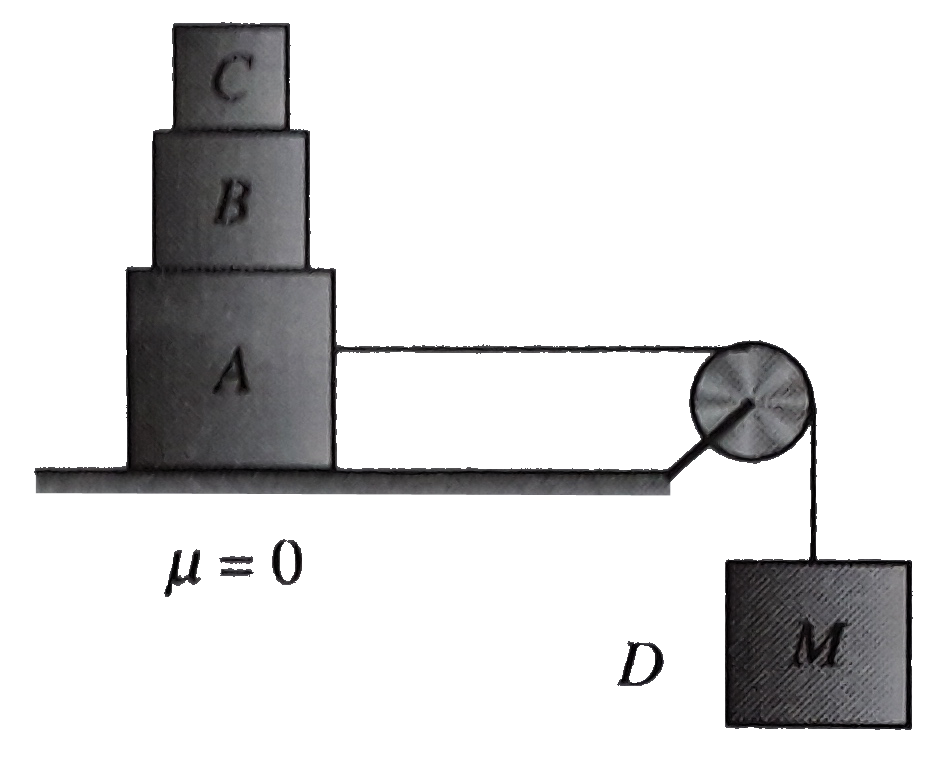
View SolutionThere block A B ,and C of equal mass m are placed one over the other on a frictionless surface (table) as shown in figure The coefficient of friction between any blocks A ,B and C is μ The maximum value of mass of block D so that the blocks A,B and C move without slipping over each other is
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View Solution
