A block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
F2t2m
F2t22m
(F2t23m)
Ft2m
The correct Answer is:B
To find the kinetic energy of a block of mass m after being acted upon by a force F for a time t, we can follow these steps:
Step 1: Understand the relationship between force, mass, and acceleration
According to Newton's second law, the force F acting on an object is equal to the mass m of the object multiplied by its acceleration a:
F=m⋅a
From this, we can express acceleration as:
a=Fm
Step 2: Relate acceleration to velocity
Since the block starts from rest, we can use the kinematic equation that relates acceleration to change in velocity over time:
v=u+at
Where u is the initial velocity (which is 0 since the block is at rest), thus:
v=0+(Fm)t=Ftm
Step 3: Calculate the momentum
The momentum p of the block can be calculated using the formula:
p=m⋅v
Substituting the expression for v:
p=m⋅(Ftm)=Ft
Step 4: Use the momentum to find kinetic energy
The kinetic energy KE of the block is given by the formula:
KE=12mv2
Substituting v from Step 2:
KE=12m(Ftm)2
This simplifies to:
KE=12m⋅F2t2m2=F2t22m
Final Answer
Thus, the kinetic energy of the block after time t is:
KE=F2t22m
According to Newton's second law, the force F acting on an object is equal to the mass m of the object multiplied by its acceleration a:
F=m⋅a
From this, we can express acceleration as:
a=Fm
Since the block starts from rest, we can use the kinematic equation that relates acceleration to change in velocity over time:
v=u+at
Where u is the initial velocity (which is 0 since the block is at rest), thus:
v=0+(Fm)t=Ftm
The momentum p of the block can be calculated using the formula:
p=m⋅v
Substituting the expression for v:
p=m⋅(Ftm)=Ft
The kinetic energy KE of the block is given by the formula:
KE=12mv2
Substituting v from Step 2:
KE=12m(Ftm)2
This simplifies to:
KE=12m⋅F2t2m2=F2t22m
Thus, the kinetic energy of the block after time t is:
KE=F2t22m
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Check points
50 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
Two bodies of masses m1 and m2 are acted upon by a constant force F for a time t . They start from rest and acquire kinetic energies K1 and K2 respectively. Then K1K2 is :
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View Solution
Knowledge Check
Two bodies A and B have masses 20 kg and 5 kg respectively. Each one is acted upon by a force of 4 kg wt. If they acquire the same kinetic energy in times tA and tB, then the ratio tAtB is
A12B2C25D56
A block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA block of mass 20 kg is acted upon by a force F=30N at an angle 53∘ with horizontal in downward direction as shown. The coefficient of friction between the block and the forizontal surface is 0.2. The friction force acting on the block by the ground is (g=10ms2)
View SolutionA bullet of mass m moving with velocity v strikes a block of mass M at rest and gets embedded into it. The kinetic energy of the composite block will be
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionThe velocity of a block of mass 2kg moving along x− axis at any time t is givne by v=20−10t(m/s) where t is in seconds and v is in m/s. At time t=0, the block is moving in positive x− direction.
The Kinetic energy of block at t=3sec. is :
View SolutionA block of mass m is kept on an another block of mass M. The coefficient of friction between the blocks varies as μ=(μ0+kx) while friction between lower block and ground is zero. A time varying force F = 10t is applied horizontally on the upper block. Find time t0 when relative motion will start between the blocks. (x is relative displacement between the blocks.)
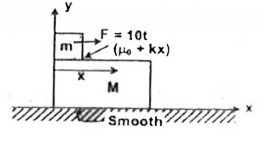
View Solution
