A block rests on a rough plane whose inclination θ to the horizontal can be varied. Which of the following graphs indicates how the friction force F between the block and the plane varies as θ is increased?
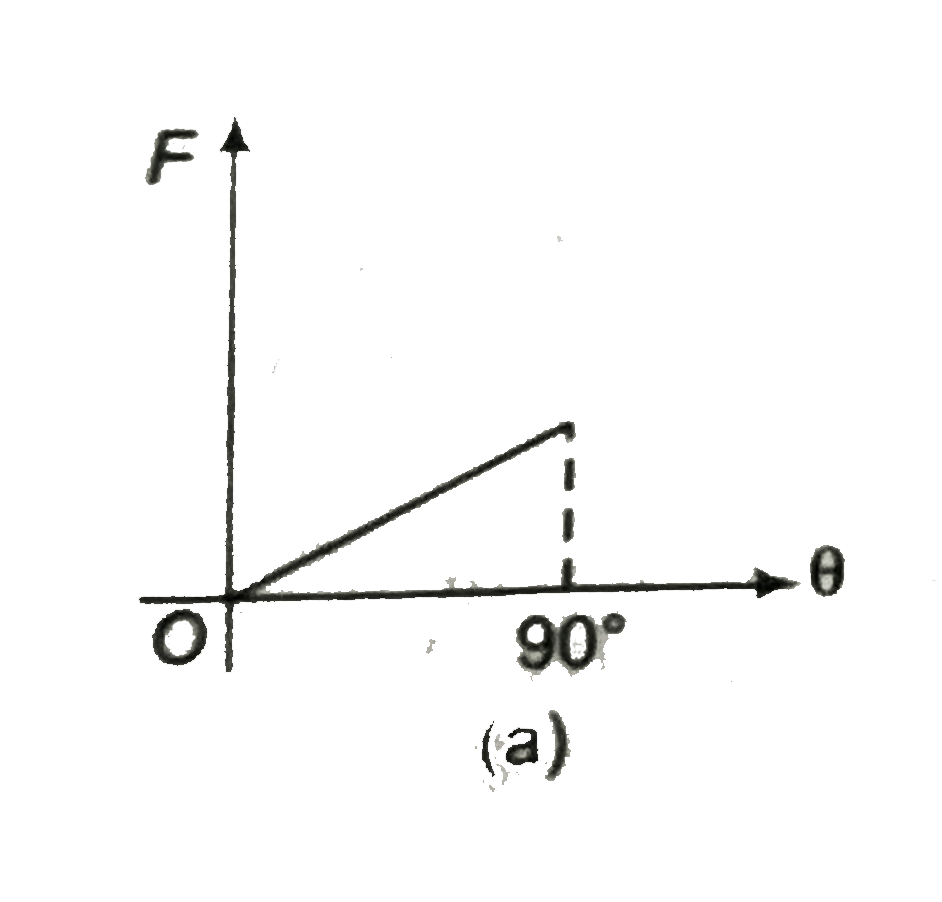
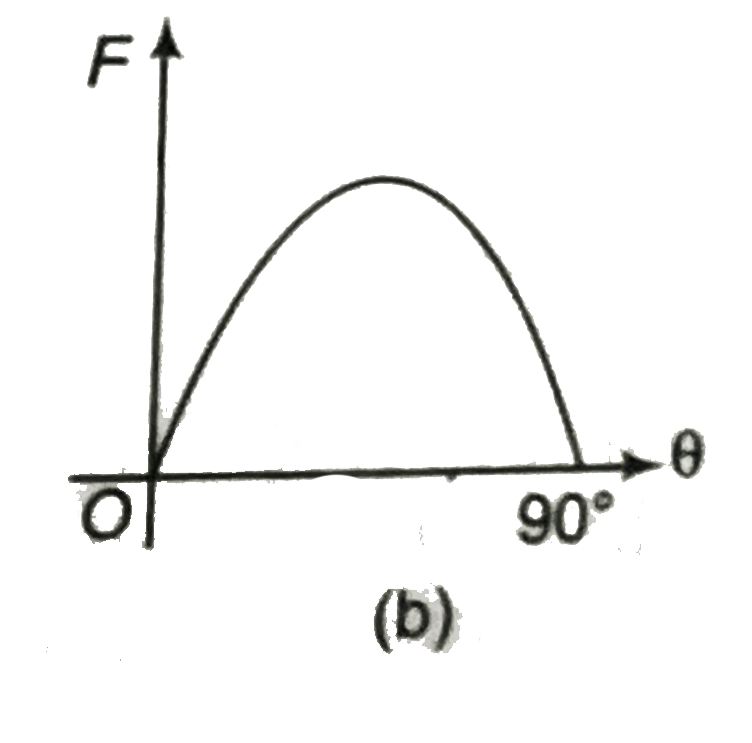
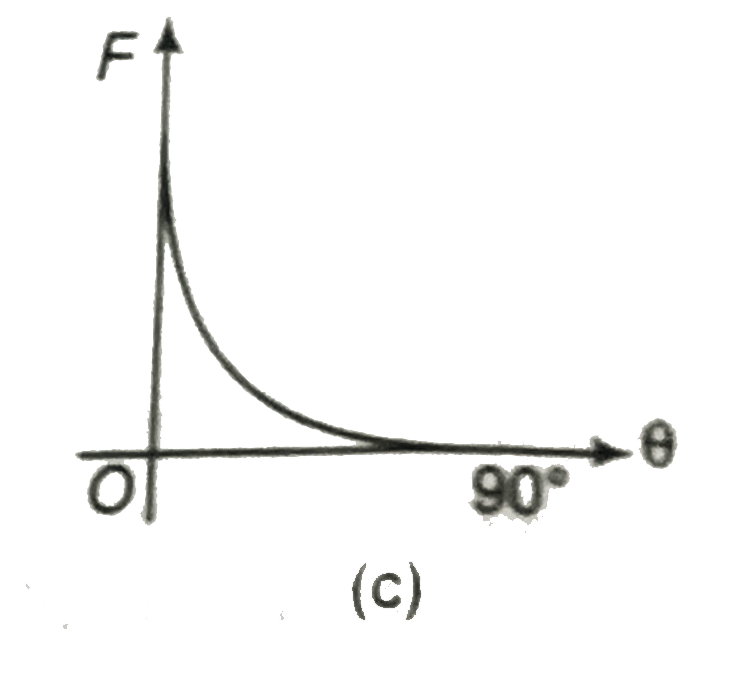
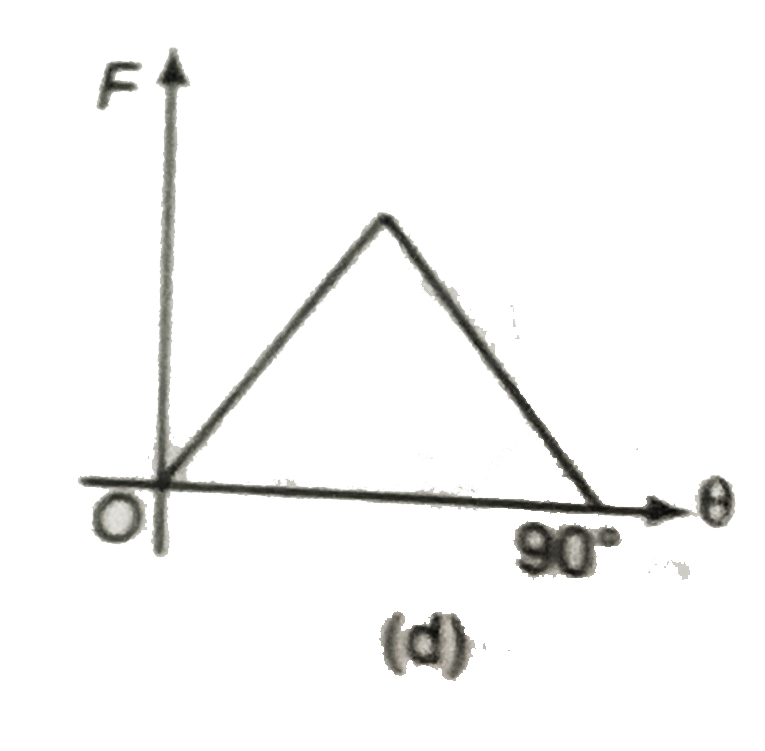
The correct Answer is:B
Let α= angle of repose
For θ≤α Block is stationary and force of friction,
f=mgsinθ
or f∝sinθ
i.e. it is sine graph
For θ≥α Block sides downwards
f=μmgsinθ
or f∝cosθ
i.e. it is cosine graph
the correct alternative is therefore (b).
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of g5 ?
View Solution
Knowledge Check
A body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the contact force between the block and the plane
 Aremains constantBdecreases.Cfirst decreases then increasesDfirst increases then decrease.
Aremains constantBdecreases.Cfirst decreases then increasesDfirst increases then decrease.A block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
Aμmg2tsinθBmg2t(sinθ−μcosθ)Cμmg2tcosθ(sinθ−μcosθ)Dμmg2tcosθA body is placed on a rough inclined plane of inclination θ. As the angle θ is the increased from 0∘ to 90∘, the normal force between the block and the plane is,
 AF+mgtanθBFcosθ−mgsinθCFsinθ−mgcosθDFsinθ+mgcosθ
AF+mgtanθBFcosθ−mgsinθCFsinθ−mgcosθDFsinθ+mgcosθ
A block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
View SolutionA body is placed on a rough inclined plane of inclination θ. As the angle θ is increased from 0∘ to 90∘ the contact force between the block and the plane
View SolutionA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .
.
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View Solution