A bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
The correct Answer is:C
To solve the problem step by step, we will calculate the net acceleration of the bob suspended from the string when it makes an angle of 60 degrees with the vertical.
Step 1: Identify the given values
- Mass of the bob, m=1kg
- Length of the string (which acts as the radius), R=1m
- Speed of the bob, V=4m/s
- Angle with the vertical, θ=60∘
Step 2: Calculate the centripetal acceleration
Centripetal acceleration (ac) is given by the formula:
ac=V2R
Substituting the values:
ac=(4m/s)21m=161=16m/s2
Step 3: Determine the tangential acceleration
To find the tangential acceleration (at), we need to calculate the component of the gravitational force acting along the direction of motion. The gravitational force acting on the bob is mg, where g is the acceleration due to gravity (approximately 10m/s2).
The tangential component of the gravitational force can be calculated as:
Ft=mgsin(θ)
Substituting the values:
Ft=1kg⋅10m/s2⋅sin(60∘)
Using sin(60∘)=√32:
Ft=10⋅√32=5√3N
Now, the tangential acceleration is given by:
at=Ftm=5√31=5√3m/s2
Step 4: Calculate the net acceleration
The net acceleration (a) is the vector sum of the centripetal acceleration and the tangential acceleration. It can be calculated using the Pythagorean theorem:
a=√a2c+a2t
Substituting the values:
a=√(16m/s2)2+(5√3m/s2)2
Calculating each term:
=√256+(5√3)2
=√256+75=√331
Calculating the square root:
≈18.2m/s2
Final Answer
The net acceleration of the bob at the instant when the string makes an angle of 60∘ with the vertical is approximately 18.2m/s2.
---
- Mass of the bob, m=1kg
- Length of the string (which acts as the radius), R=1m
- Speed of the bob, V=4m/s
- Angle with the vertical, θ=60∘
Centripetal acceleration (ac) is given by the formula:
ac=V2R
Substituting the values:
ac=(4m/s)21m=161=16m/s2
To find the tangential acceleration (at), we need to calculate the component of the gravitational force acting along the direction of motion. The gravitational force acting on the bob is mg, where g is the acceleration due to gravity (approximately 10m/s2).
Ft=mgsin(θ)
Substituting the values:
Ft=1kg⋅10m/s2⋅sin(60∘)
Using sin(60∘)=√32:
Ft=10⋅√32=5√3N
at=Ftm=5√31=5√3m/s2
The net acceleration (a) is the vector sum of the centripetal acceleration and the tangential acceleration. It can be calculated using the Pythagorean theorem:
a=√a2c+a2t
Substituting the values:
a=√(16m/s2)2+(5√3m/s2)2
Calculating each term:
=√256+(5√3)2
=√256+75=√331
Calculating the square root:
≈18.2m/s2
The net acceleration of the bob at the instant when the string makes an angle of 60∘ with the vertical is approximately 18.2m/s2.
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Matrix Matching
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Integer
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - More than One Option is Correct
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Upto what maximum height will the bob rise with respect to the bottommost point ?
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
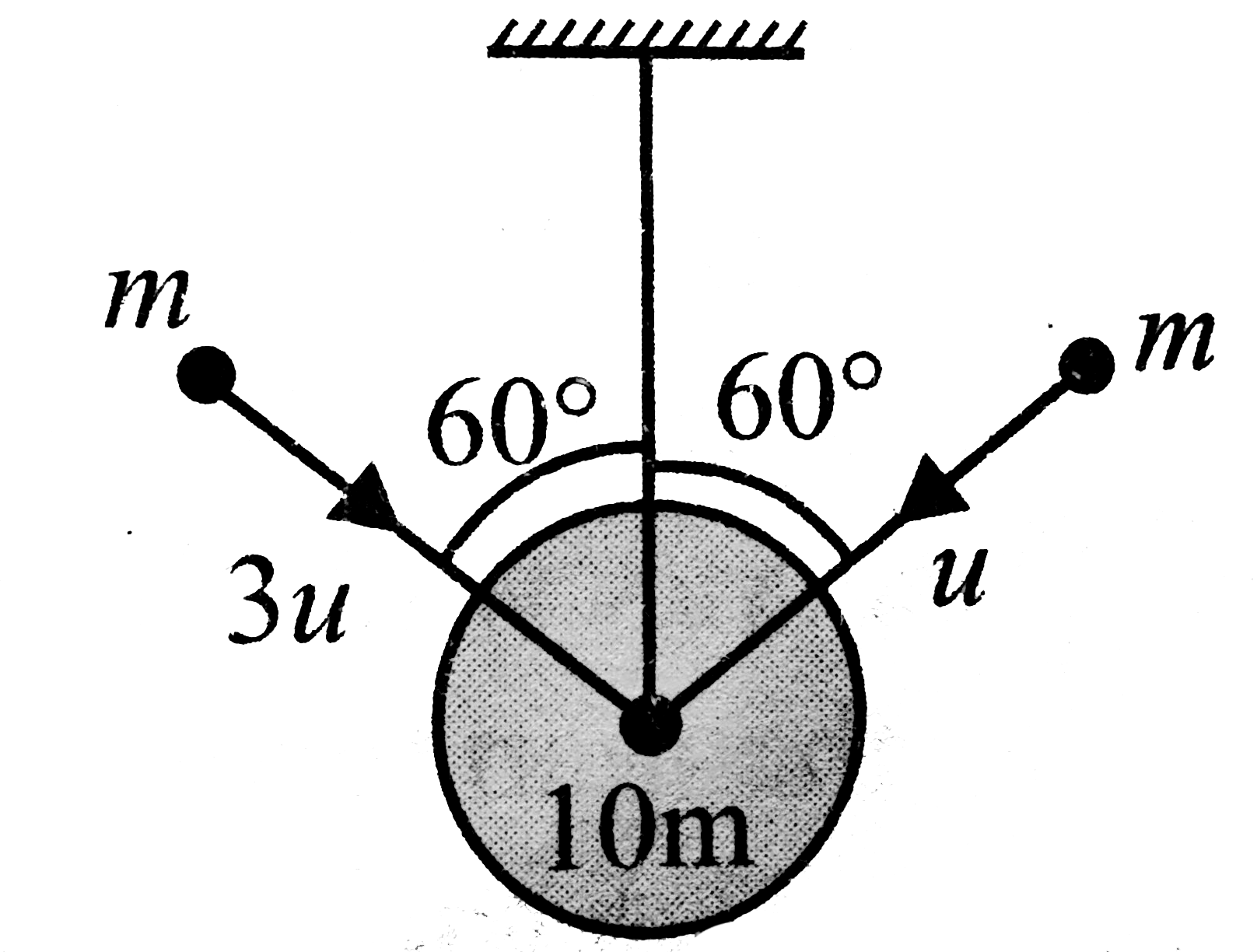
View SolutionA bob of mass 10m is suspended through an inextensible string of length l. When the bob is at rest in equilibrium position, two particles, each of mass m, strike it as shown in Fig. The particles stick after collision. Choose the correct statement from the following:
View SolutionA bob of mass m=50g is suspended form the ceiling of a trolley by a light inextensible string. If the trolley accelerates horizontally, the string makes an angle 37∘ with the vertical. Find the acceleration of the trolley.

View SolutionThe bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View SolutionA bob of mass 0.1 kg hung from the ceiling of a room by a string 2 m long is set into oscillation The speed of the bob at its mean position 1m/s What is the trajectory of the bob if the string is cut when the bob is (a) at one of its extreme position (b) at is mean position ?
View SolutionOne end of ideal string tied up with fixed suppot & other end is tied with a bob. The string is released from horizontal position. When string makes an angle of θ with vertically downward direction then the acceleration vector of bob is horizontal then θ is
View SolutionA block of mass 10kg is suspended from string of length 4m. When pulled by a force F along horizontal from midpoint. Upper half of string makes 45∘ with vertical, value of F is
View SolutionA bullet ofmass m is fired with a velocity 10m/s at angle θ with horizontal. At the hightest point of its trajectory, it collsides head-on with a bob of mass 3m suspended by a massless string of length 2/5m and gets embedded in the bob. After th collision the string moves through an angle of 60∘.
The vertical coordinate of the initial positon of the bob w.r.t. the point of firing of the bullet is
View SolutionA bob is suspended from an ideal string of length 'l'. Now it is pulled to a side through 60∘ to vertical and whirled along a horizontal circle. Then its period of revolution is
View Solution
