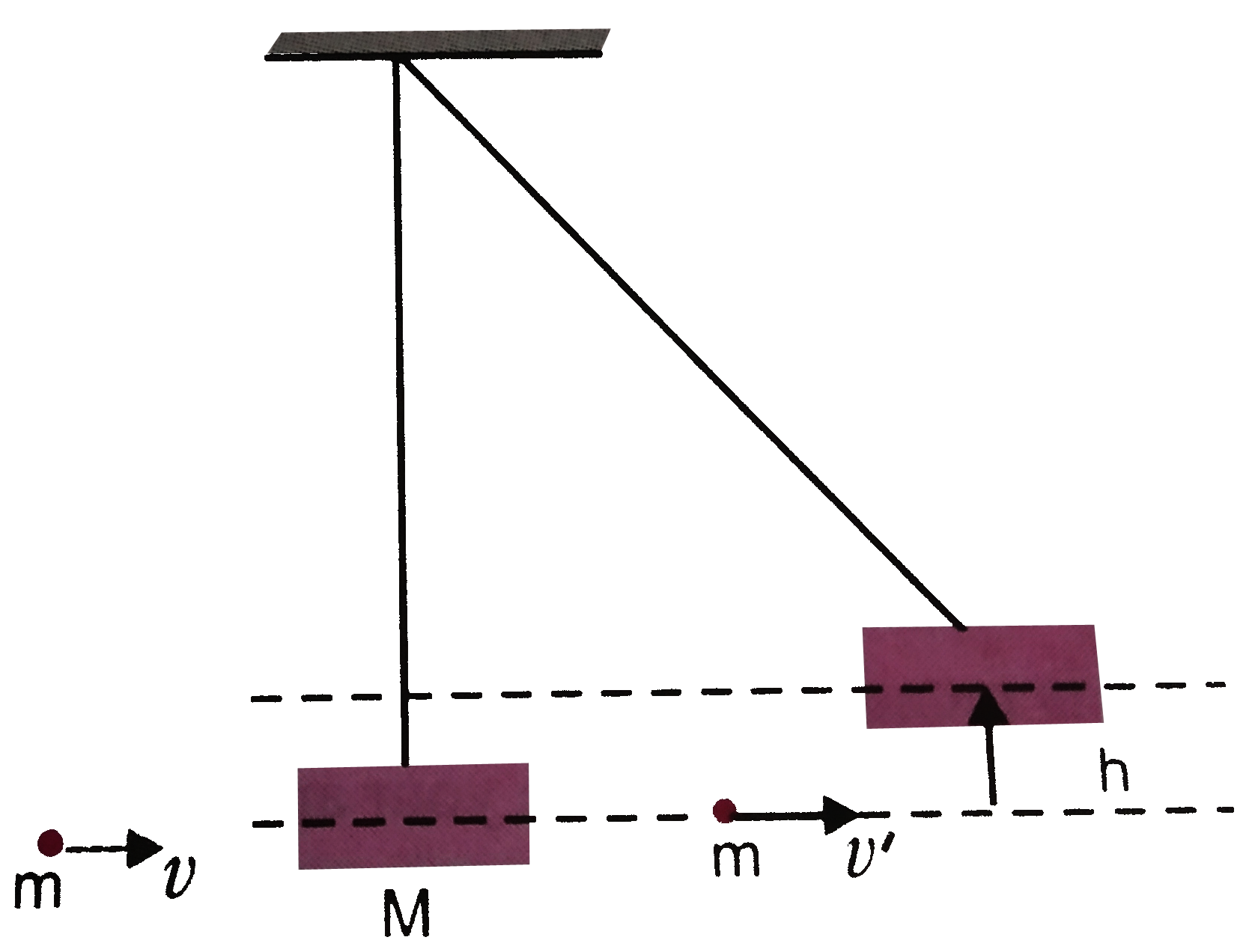
A bullet of mass 20 g moving horizontally at a speed of 300 m/s is fired into a wooden block of mass 500 g suspended by a long string. The bullet crosses the block and emerges on the other side. If the centre of mass of the block rises through a height of 20.0 cm, find the speed of the bullet as it emerges from the block.
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a bullet of mass m1=20g=0.02kg moving with an initial speed u1=300m/s. It strikes a wooden block of mass m2=500g=0.5kg which is suspended and can move vertically. After the bullet passes through the block, the block rises to a height h=20cm=0.2m. We need to find the speed of the bullet as it emerges from the block, denoted as v′.
Step 2: Calculate the initial velocity of the block after the bullet passes through
When the block rises to a height h, we can use the principle of conservation of energy. The potential energy gained by the block is equal to the kinetic energy it had just after the bullet passed through.
The potential energy (PE) gained by the block is given by:
PE=m2gh
where g=9.81m/s2.
Substituting the values:
PE=0.5×9.81×0.2=0.981J
This potential energy is equal to the kinetic energy (KE) of the block just after the bullet passes through:
KE=12m2v2
Setting the two equal:
0.981=12×0.5×v2
0.981=0.25v2
v2=0.9810.25=3.924
v=√3.924≈1.98m/s
Step 3: Apply the conservation of momentum
Before the collision, the total momentum of the system (bullet + block) is:
pinitial=m1u1+m2⋅0=0.02×300+0=6kg m/s
After the bullet passes through the block, the total momentum is:
pfinal=m1v′+m2v
Substituting the known values:
6=0.02v′+0.5×1.98
Calculating the second term:
6=0.02v′+0.99
Rearranging gives:
0.02v′=6−0.99=5.01
v′=5.010.02=250.5m/s
Conclusion
The speed of the bullet as it emerges from the block is approximately v′≈250.5m/s.
---
We have a bullet of mass m1=20g=0.02kg moving with an initial speed u1=300m/s. It strikes a wooden block of mass m2=500g=0.5kg which is suspended and can move vertically. After the bullet passes through the block, the block rises to a height h=20cm=0.2m. We need to find the speed of the bullet as it emerges from the block, denoted as v′.
When the block rises to a height h, we can use the principle of conservation of energy. The potential energy gained by the block is equal to the kinetic energy it had just after the bullet passed through.
PE=m2gh
where g=9.81m/s2.
PE=0.5×9.81×0.2=0.981J
KE=12m2v2
Setting the two equal:
0.981=12×0.5×v2
0.981=0.25v2
v2=0.9810.25=3.924
v=√3.924≈1.98m/s
Before the collision, the total momentum of the system (bullet + block) is:
pinitial=m1u1+m2⋅0=0.02×300+0=6kg m/s
pfinal=m1v′+m2v
Substituting the known values:
6=0.02v′+0.5×1.98
Calculating the second term:
6=0.02v′+0.99
Rearranging gives:
0.02v′=6−0.99=5.01
v′=5.010.02=250.5m/s
The speed of the bullet as it emerges from the block is approximately v′≈250.5m/s.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass 10g moving horizontally with a velocity of 400ms−1 strickes a wooden block of mass 2kg which is suspended by a light inextensible string of length 5m. As a result, the center ofgravity of the block is found to rise a vertical distance of 10cm . The speed of the bullet after it emerges out hirizontally from the block will be
View SolutionA bullet of mass 0.01kg and travelling at a speed of 500ms−1 strikes a block of mass 2kg which is suspended by a string of length 5m. The centre of gravity of the block is found to raise a vertical distance of 0.2m. What is the speed of the bullet after it emerges from the block?
View SolutionA bullet of mass 2g travelling at a speed of 500m/s is fired into a ballistic pendulum of mass 1.0kg suspended from a cord 1.0m long. The bullet penetrates the pendulum and emerges with a velocity of 100m/s. Through what vertical height will the pendulum rise?
View SolutionA bullet of mass 0.01 kg and travelling at a speed of 500 m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The center of gravity of the block is found to rise a vertical distance of 0.1m, figure. What is the speed of the bullet after it emerges from the block ? (g=9.8m/s2).
View SolutionA bullet of mass 50g if fired from below into the bob of mass 450g of a long simple pendulum as shown in Fig. The bullet remains inside the bob and the bob rises through a height of 1.8m. Find the speed of the bullet.Take g=10ms2
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View SolutionA bullet of mass 25 g is fired horizontally into a ballistic pendulum of mas 5.0 kg and gets embedded in it figure. If the centre of the pendulum rises by a distance of 10 cm, find the speed of the bullet.
View SolutionA bullet of mass 20 g travelling horizontally with a speed of 500 m/s passes through a wooden block of mass 10.0 kg initially at rest on a level surface. The bulet emerges with speed of 100 m/s and the block slides 20 cm on the surface before coming to rest. Find the friction cioefficient between the block and the surface figure.

View SolutionA 4.00g bullet travelling horizontally with a velocity of magnitude 500m/s is fired into a wooden block with a mass of 1.00kg, initially at rest on a level surface. The bullet passes through the block and emerges with speed 100m/s. The block slides a distance of 0.30m along the surface from its initial position.
(a) What is the coefficient of kinetic friction between block and surface?
(b) What is the decrease in kinetic energy of the bullet?
(c) What is the kinetic energy of the block at the instant after the bullet has passed through it? Neglect friction during collision of bullet with the block.
View Solution
