A charge Q is uniformly distributed over a rod of length ι. Condider a hypothetical cube of edge ι with the centre of the cube at one end of the rod. Find the minimum possible flux of the electric field through the entire surface of the cube.
To solve the problem, we need to find the minimum possible electric flux through the entire surface of a cube that has one end at the center of a uniformly charged rod of length l with total charge Q.
1. Understand the Configuration:
- We have a rod of length l with a total charge Q uniformly distributed along its length.
- A cube with edge length l is positioned such that its center is at one end of the rod.
2. Determine the Charge Distribution:
- Since the charge is uniformly distributed over the rod, the linear charge density λ can be calculated as:
λ=Ql
3. Identify the Charge Enclosed by the Cube:
- The cube extends from the end of the rod to a distance l into space.
- Since the cube is centered at one end of the rod, only half of the rod (length l/2) is inside the cube.
- Therefore, the charge enclosed by the cube can be calculated as:
Qenclosed=λ⋅l2=Ql⋅l2=Q2
4. Apply Gauss's Law:
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
Φ=Qenclosedϵ0
- Substituting the value of Qenclosed:
Φ=Q/2ϵ0=Q2ϵ0
5. Conclusion:
- The minimum possible electric flux through the entire surface of the cube is:
Φ=Q2ϵ0
- We have a rod of length l with a total charge Q uniformly distributed along its length.
- A cube with edge length l is positioned such that its center is at one end of the rod.
- Since the charge is uniformly distributed over the rod, the linear charge density λ can be calculated as:
λ=Ql
- The cube extends from the end of the rod to a distance l into space.
- Since the cube is centered at one end of the rod, only half of the rod (length l/2) is inside the cube.
- Therefore, the charge enclosed by the cube can be calculated as:
Qenclosed=λ⋅l2=Ql⋅l2=Q2
- According to Gauss's Law, the electric flux Φ through a closed surface is given by:
Φ=Qenclosedϵ0
- Substituting the value of Qenclosed:
Φ=Q/2ϵ0=Q2ϵ0
- The minimum possible electric flux through the entire surface of the cube is:
Φ=Q2ϵ0
Topper's Solved these Questions
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Objective 2
8 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise
8 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
Similar Questions
A charge Q is placed at the centre of a cube. Find the flux of the electric field through the six surfaced of the cube.
View SolutionA charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is

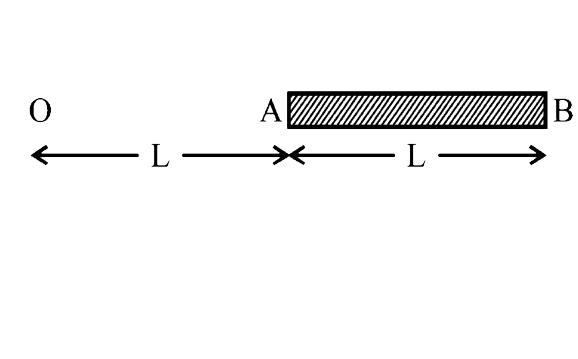
View SolutionA charge Q is uniformly distributed over a long rod AB of length L as shown in the figure. The electric potential at the point O lying at distance L from the end A is
View SolutionA Charge Q is distributed uniformly on a ring of radius r. A sphere of equal r is constructed with its centre at the periphery of the ring (figure 30.12) Find the flux of the electric field through the surface of the sphere.
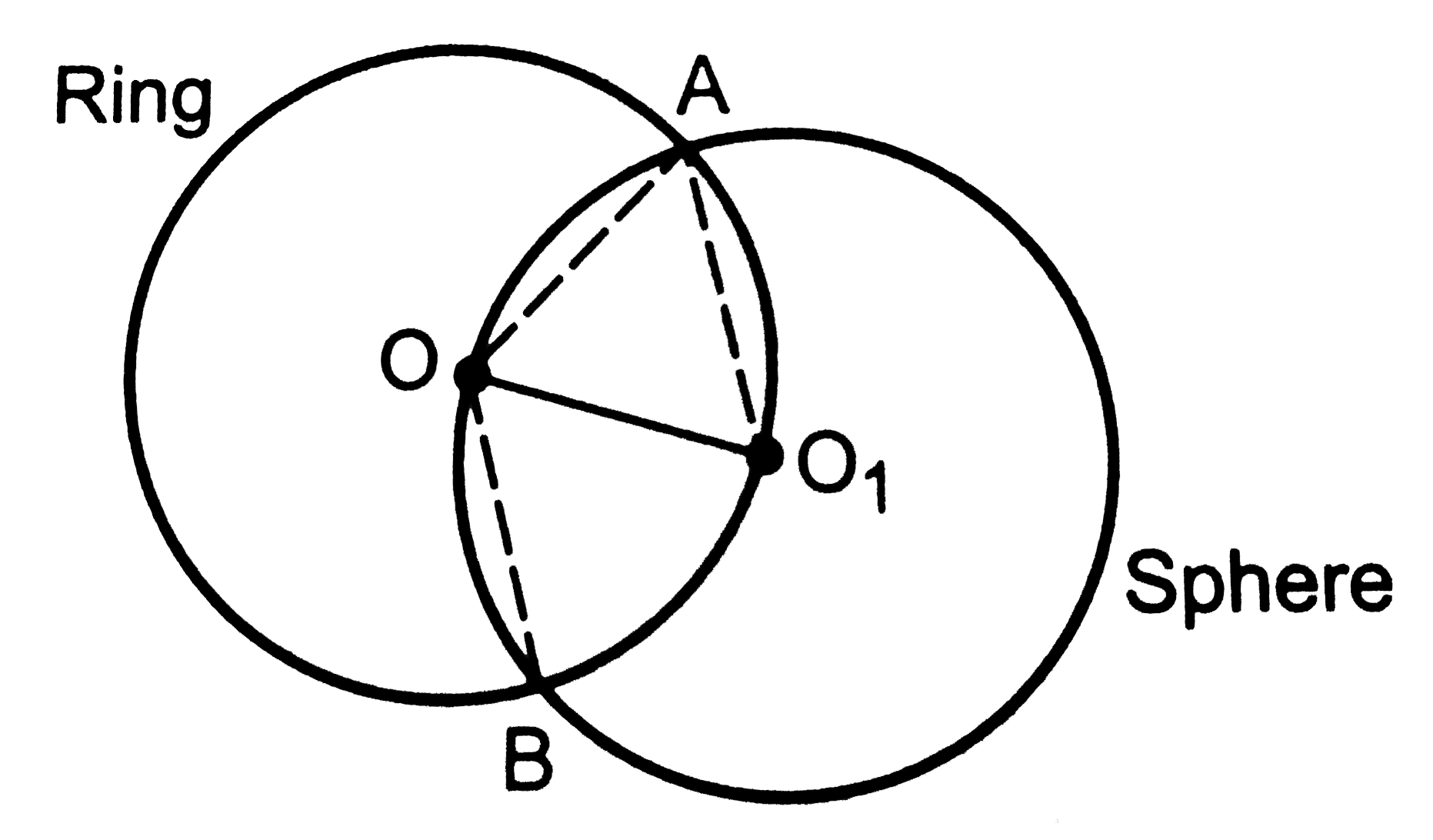
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionA charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
View SolutionA charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionA charge q is placed at the centre of a cube of side l what is the electric flux passing through two opposite faces of the cube ?
View SolutionFigure shown an imaginary cube of edge L/2. A uniformly Charged rod of length L moves towards left at a small but constant speed v. At t=0, the left end just touches the centre of the cube opposite it. Which of the graphs shown in figure represents the flux of the electic field through the cube as the rod goes through it?

View Solution
