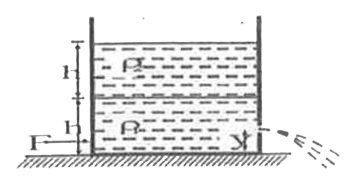
A cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (Take g = 10 ms^(-2)).
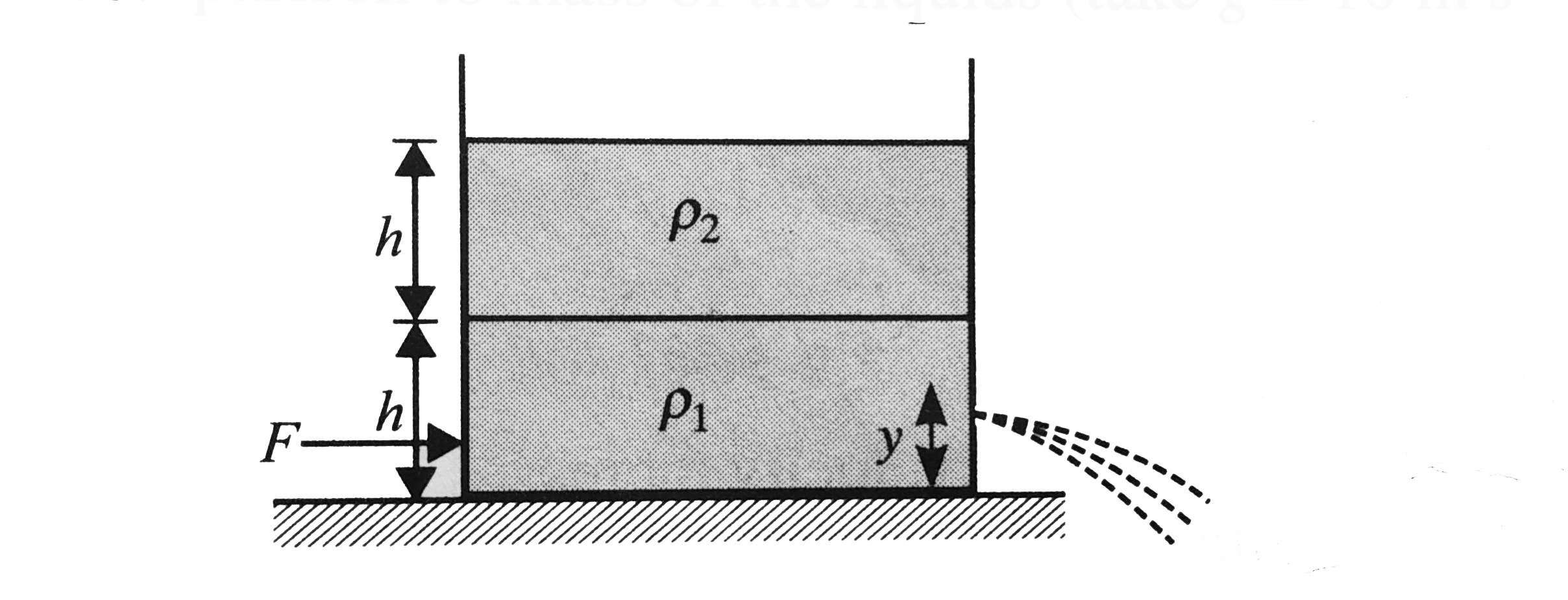
The velocity of efflux is
7.2N
10N
15.5N
20.4N
The correct Answer is:A
When the cylinder is on the smooth horizontal plane, force F required to keep the cylinder statioinary equals horizontal thrust exerted by fluid jet . But that is equal to mass flowing per second × change in velocity of this mass.
∴F=(avρ)(v−0)=aρv2 or F=7.2N
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - True/False
1 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - SCQ_TYPE
13 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg = 10 ms^(-2)).
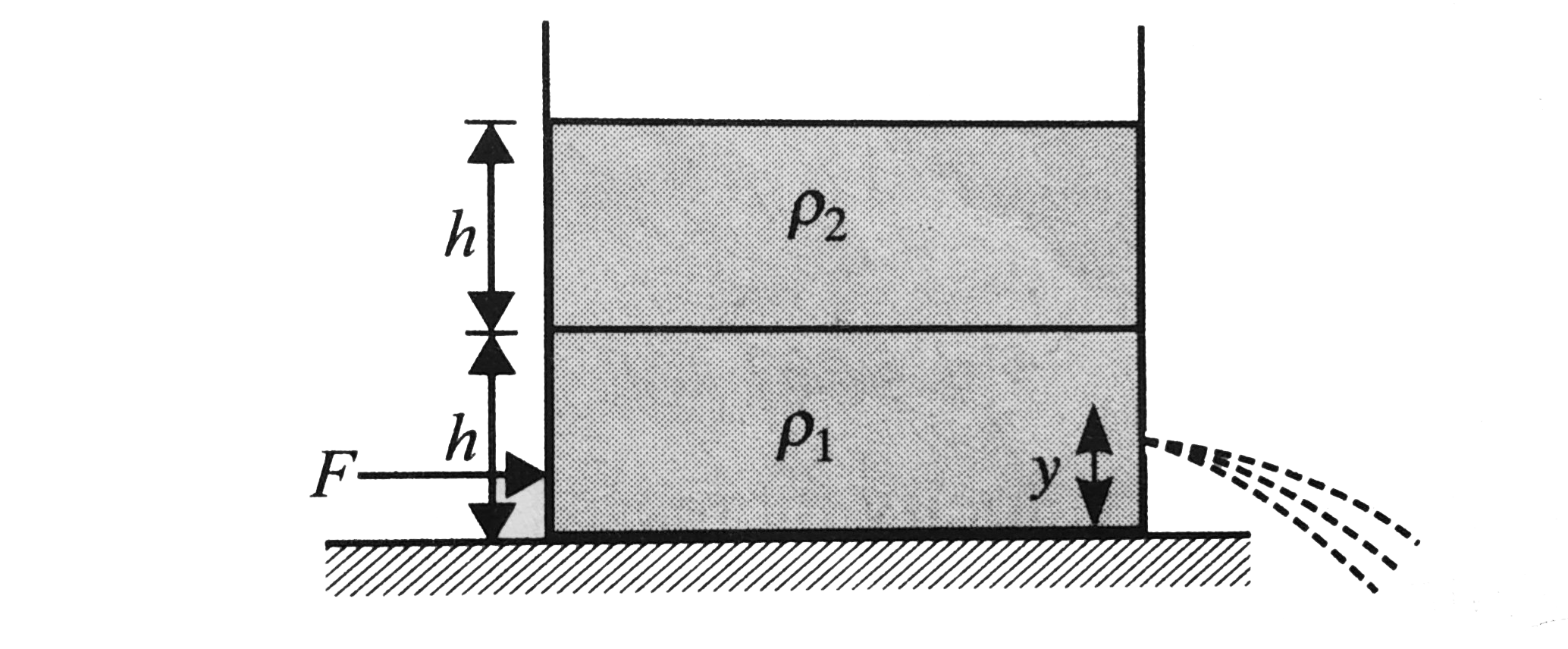
The horizontal force required to keep the cylinder in static equilibrium, on a smooth horizontal plane is
View SolutionA cylindrical tank having cross-sectional area A=0.5m2 is filled with two liquids of density ρ1=900kgm−3 and ρ2=600kgm−3, to a height h=60cm each as shown in the figure. A small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids (akeg=10ms−2).
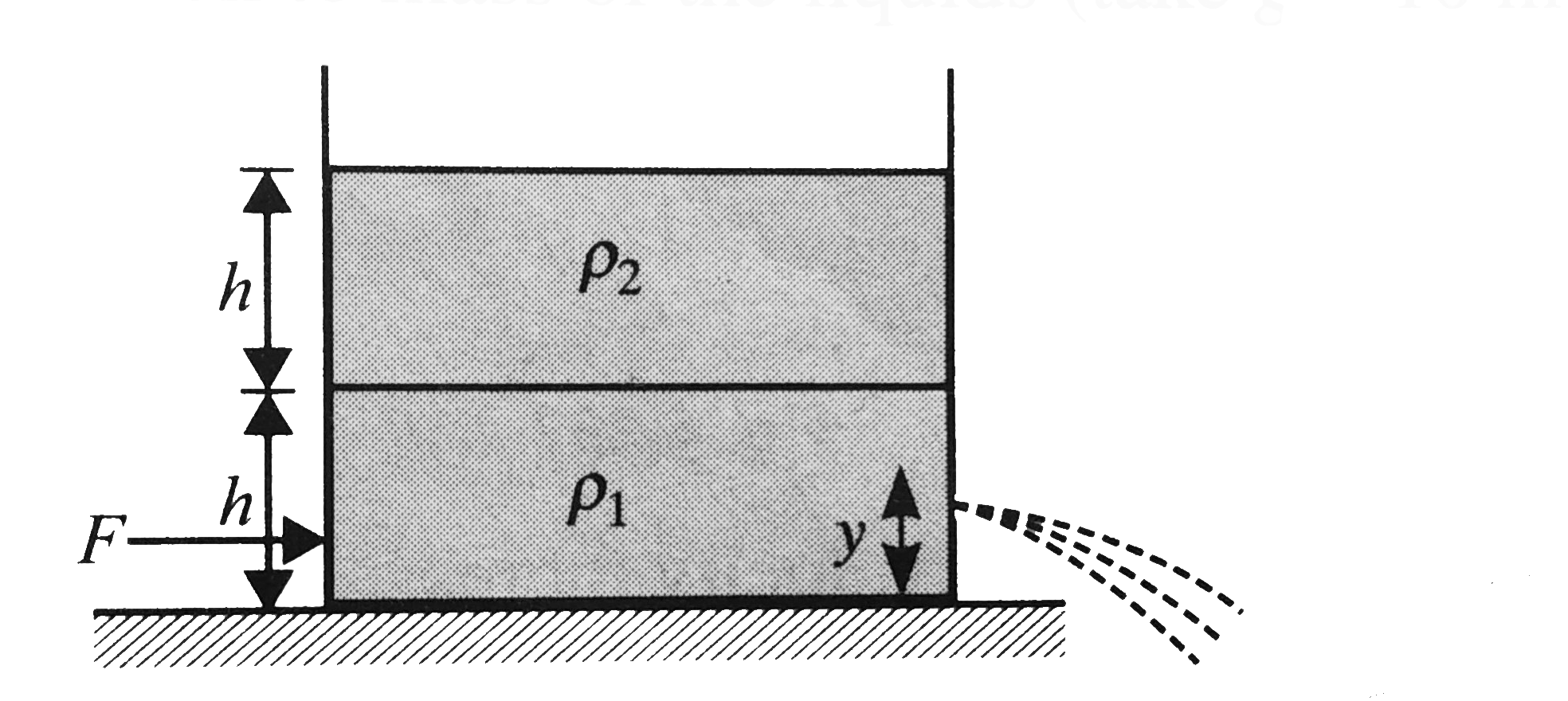
(i) horizontal force F to keep the cylinder in static equilibrium, if it is placed on a smooth horizontal plane and (ii) minimum and maximum values of F to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is µ = 0.01. (g = 10 ms –2 )
View SolutionA cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height h =60cm2each.A small hole having area a=5 cm^2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
Horizontal force F to keep the cylinder in static equilibrium , if it is placed on a smooth horizontal thrust exerted by fluid jet . But that is equal to mass flowing per second × change in velocity of this mass
∴ F=(avρ)(v−0)=aρv2
or F=7.2N
View SolutionA cylindrical tank having cross - sectional area A=0.5m2 is filled with two liquids of density ρ1=900 kg m−3andρ2=600 kg m−3 , to a height a =6cm2 is made in right vertical wall at a height y = 20 cm from the bottom . A horizontal force F is applied on the tank to keep it in static equilibrium . The tank is lying on a horizontal surfaces . Neglect mass of cylindrical tank camparison to mass of liquids ( take g=10ms−2)
Minimum and maximum values of F to keep the cylinder in static just after the water starts to spill through the hole . If the co - efficient of static friction between contact surfaces is 0.01
View Solution_E01_229_Q01.png)
A cylinderical tank having cross sectional area ∧=0.5m2 is filled liquids of densities ρ1=900kgm3&ρ2=600kgm3 to a height h=60cm as shown in the figure a small hole having area a=5cm2 is made in right vertical wall at a height y=20cm from the bottom calculate.
(i). velocity of efflux
(ii). horizontal force F to keep the cylinder in static equilibrium if it is placed on a smooth horizontal plane
(iii). minimum and maximum value of F to keep the cylinder at rest. The coefficient of friction between cylinder and the plane is μ=0.1
(iv). velocity of the top most layer of the liquid column and also the velocity of the boundary separating the two liquids.
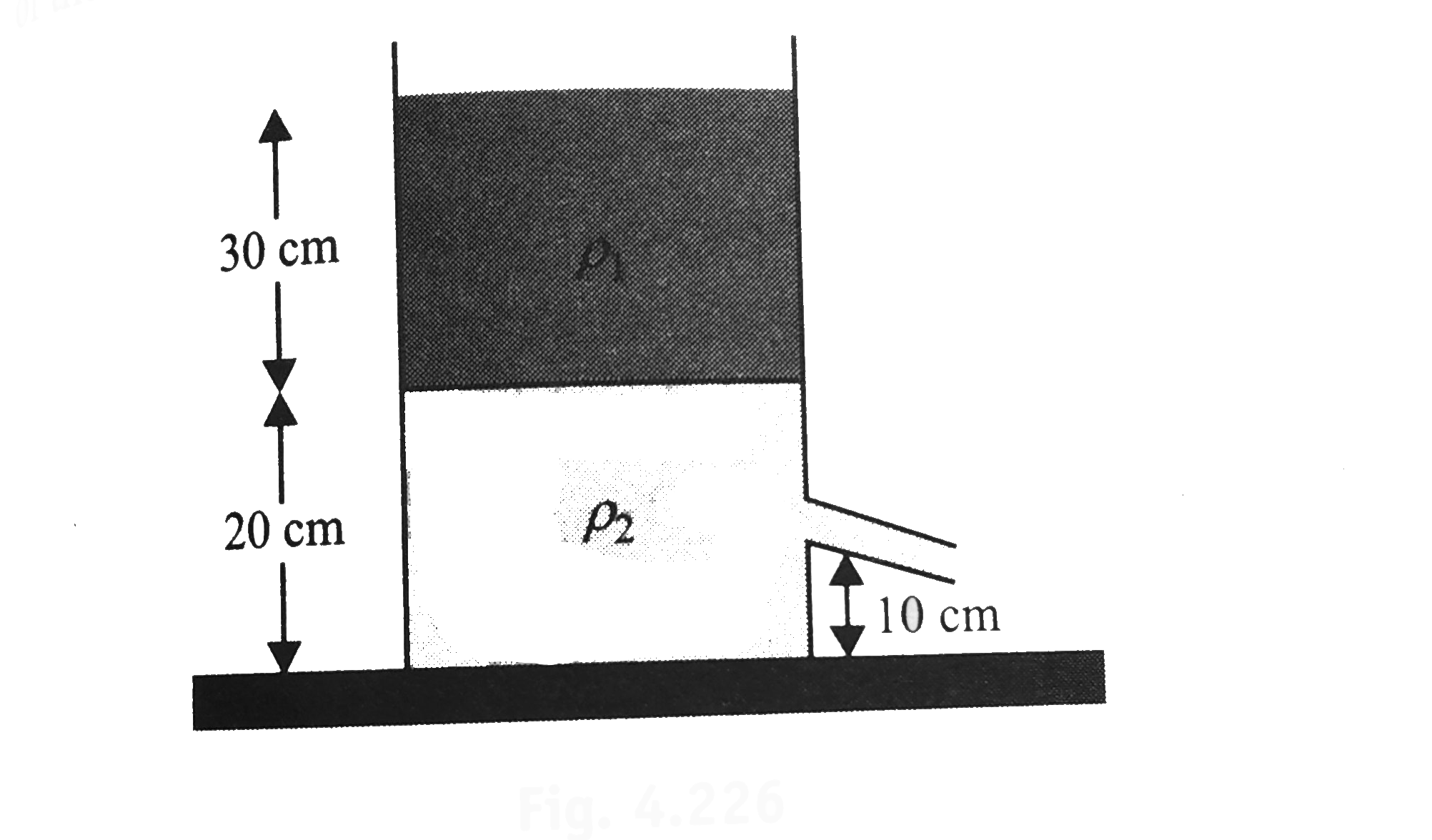
View SolutionA cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density ρ1=600kg/m3 and ρ2=1200kg/m3 as shown in the figure.
A small hole having cross sectional area 5cm2 is made in right side vertical wall as shown. Take atmospheric pressure as p0=105N/m2,g=10m/s2. For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm2. Neglect the mass of the vessel.
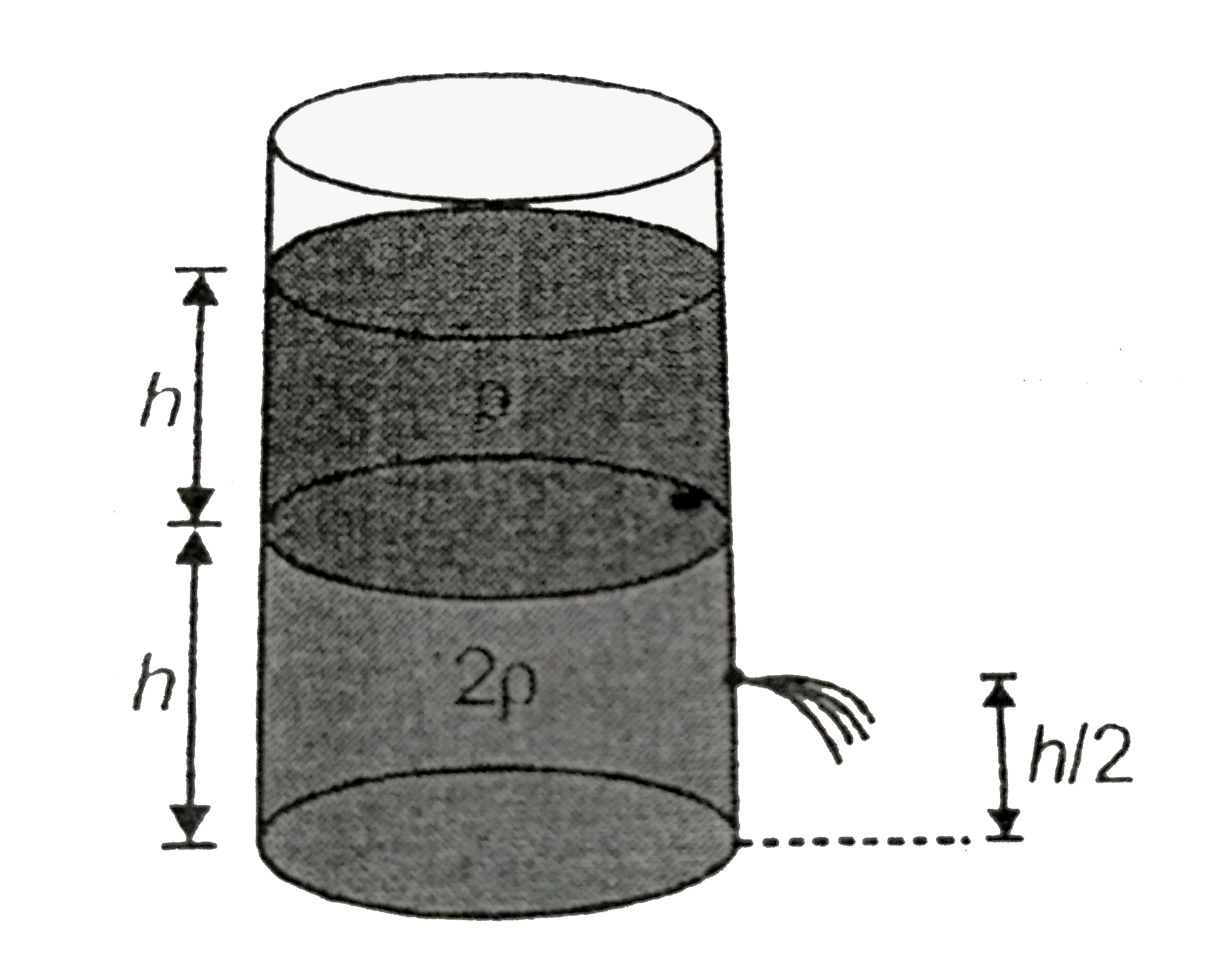
View SolutionA vessel is filled with two different liquids of densities ρand2ρ respectively as shown in the figure. The velocity of flow of liquid through a hole at height h2 from bottom is
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA cube of 1 kg is floating at the interface of two liquids of density ρ1=3/4gm/cm3andρ2=2.5gm/cm3 The cube has (3/5)th part in ρ2 and (2/5)th part in ρ1 .Find the density of the cube .

View SolutionA hole is made at the bottom of the tank filled with water (density =1000kgm−3). If the total pressure at the bottom of the tank is three atmospheres (1 atmosphere =105Nm−2), then the velocity of efflux is nearest to
View Solution
