Question

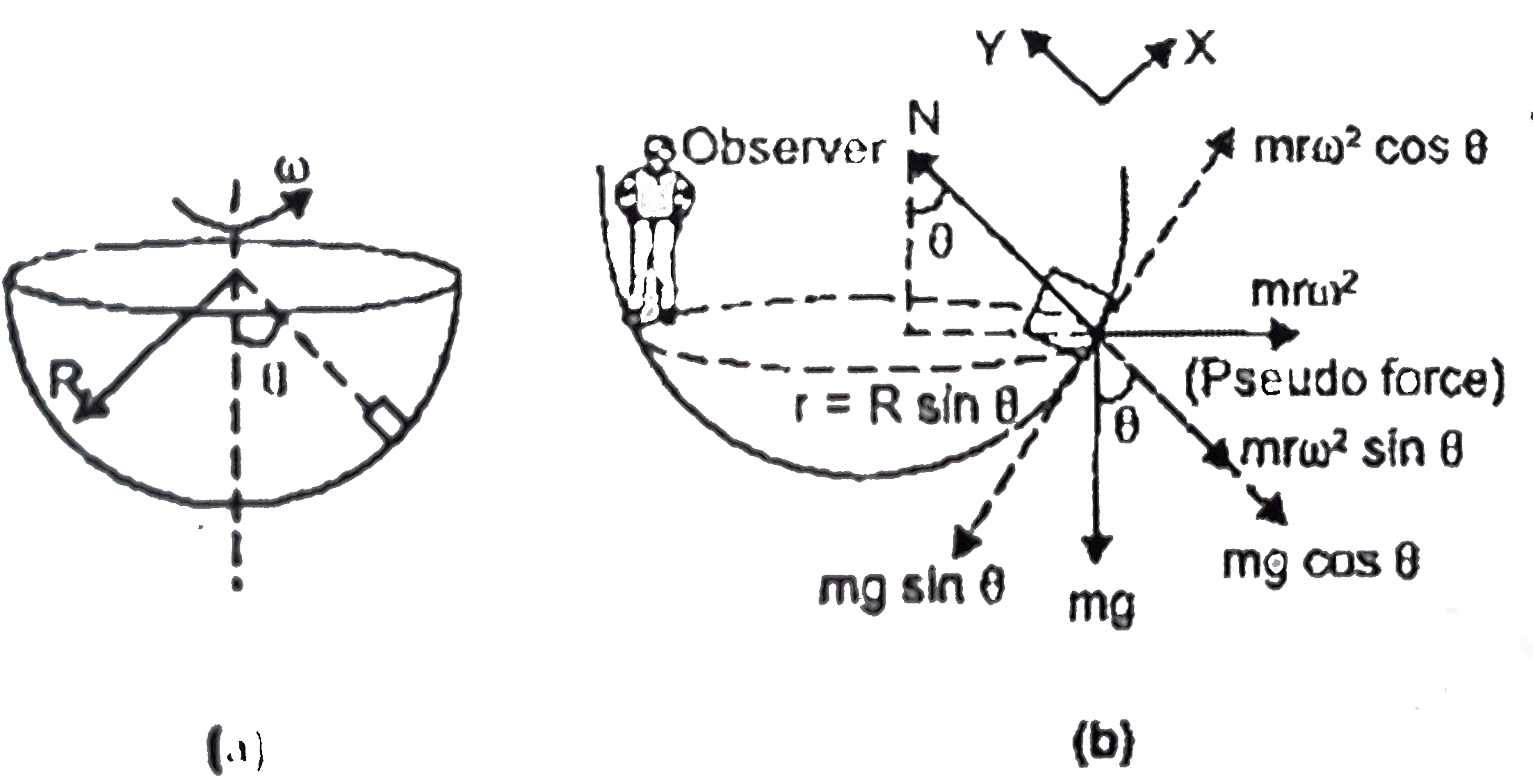
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is $\theta$, find the angular speed at which the bowl is rotating.

Explanation

To solve the problem of finding the angular speed at which a hemispherical bowl of radius $$R$$ is rotating, with a small block inside it making an angle $$\theta$$ with the vertical, we can follow these steps:

Step 1: Understand the Forces Acting on the Block
The block experiences two main forces:
1. The gravitational force \( mg \) acting downwards.
2. The normal force \( N \) exerted by the surface of the bowl, acting perpendicular to the surface.

Step 2: Analyze the Geometry
The angle \( \theta \) is made by the radius through the block with the vertical. The radius of the hemisphere is \( R \), and the radius of the circular path traced by the block is \( r = R \sin \theta \).

Step 3: Set Up the Force Balance
For the block to remain in circular motion without slipping, the centripetal force required for circular motion must be provided by the horizontal component of the normal force.

- The vertical component of the normal force is \( N \cos \theta \).
- The horizontal component of the normal force provides the centripetal force, which is \( N \sin \theta \).

Step 4: Write the Equations
1. The vertical force balance gives:
\( N \cos \theta = mg \quad \text{(1)} \)
2. The horizontal force balance (centripetal force) gives:
\( N \sin \theta = m \omega^2 r \quad \text{(2)} \)
where \( r = R \sin \theta \).

Step 5: Substitute \( r \) in the Centripetal Force Equation
Substituting \( r \) in equation (2):
\( N \sin \theta = m \omega^2 (R \sin \theta) \)

Step 6: Divide the Two Equations
Dividing equation (2) by equation (1):
\( \frac{N \sin \theta}{N \cos \theta} = \frac{m \omega^2 (R \sin \theta)}{mg} \)
This simplifies to:
\( \tan \theta = \frac{\omega^2 R \sin \theta}{g} \)

Step 7: Solve for Angular Speed \( \omega \)
Rearranging gives:
\( \omega^2 = \frac{g \tan \theta}{R \sin \theta} \)
Thus,
\( \omega = \sqrt{\frac{g \tan \theta}{R \sin \theta}} \)

Final Result
The angular speed \( \omega \) at which the bowl is rotating is given by:
\( \omega = \sqrt{\frac{g \sin \theta}{R \cos \theta}} \)