A hollow sphere of volume V is floating on water surface with half immersed in it. What should be the minimum volume of water poured inside the sphere so that the sphere now sinks into the water ?
V/2
V/3
V/4
V
The correct Answer is:A
To solve the problem of determining the minimum volume of water that needs to be poured inside a hollow sphere so that it sinks completely in water, we can follow these steps:
1. Understand the Initial Condition:
The hollow sphere has a volume V and is floating on water with half of its volume immersed. This means that the volume of water displaced by the sphere is V2.
2. Apply Archimedes' Principle:
According to Archimedes' principle, the buoyant force acting on the sphere is equal to the weight of the water displaced. The weight of the water displaced can be expressed as:
Fb=Volume of water displaced×Density of water×g=V2⋅ρ⋅g
where ρ is the density of water and g is the acceleration due to gravity.
3. Calculate the Weight of the Sphere:
The weight of the sphere can be expressed as:
Ws=m⋅g
where m is the mass of the sphere.
4. Determine the Weight After Adding Water:
Let V0 be the volume of water added to the sphere. The weight of the sphere after adding water becomes:
W′s=m⋅g+V0⋅ρ⋅g
5. Condition for Sinking:
For the sphere to sink completely, the weight of the sphere plus the weight of the water inside must equal the buoyant force when the sphere is fully submerged. The buoyant force when fully submerged is:
F′b=V⋅ρ⋅g
6. Set Up the Equation:
We set the total weight equal to the buoyant force:
m⋅g+V0⋅ρ⋅g=V⋅ρ⋅g
7. Simplify the Equation:
Dividing through by g (assuming g≠0):
m+V0⋅ρ=V⋅ρ
8. Rearranging for V0:
Rearranging gives:
V0⋅ρ=V⋅ρ−m
Thus,
V0=V⋅ρ−mρ
9. Using the Initial Condition:
Since the sphere is floating half immersed, we know that:
m=V2⋅ρ
Substituting this into the equation for V0:
V0=V⋅ρ−V2⋅ρρ=V⋅ρ−V2⋅ρρ=V2
10. Conclusion:
Therefore, the minimum volume of water that needs to be poured inside the sphere for it to sink completely is:
V0=V2
Final Answer:
The minimum volume of water that needs to be poured inside the sphere is V2.
The hollow sphere has a volume V and is floating on water with half of its volume immersed. This means that the volume of water displaced by the sphere is V2.
According to Archimedes' principle, the buoyant force acting on the sphere is equal to the weight of the water displaced. The weight of the water displaced can be expressed as:
Fb=Volume of water displaced×Density of water×g=V2⋅ρ⋅g
where ρ is the density of water and g is the acceleration due to gravity.
The weight of the sphere can be expressed as:
Ws=m⋅g
where m is the mass of the sphere.
Let V0 be the volume of water added to the sphere. The weight of the sphere after adding water becomes:
W′s=m⋅g+V0⋅ρ⋅g
For the sphere to sink completely, the weight of the sphere plus the weight of the water inside must equal the buoyant force when the sphere is fully submerged. The buoyant force when fully submerged is:
F′b=V⋅ρ⋅g
We set the total weight equal to the buoyant force:
m⋅g+V0⋅ρ⋅g=V⋅ρ⋅g
Dividing through by g (assuming g≠0):
m+V0⋅ρ=V⋅ρ
Rearranging gives:
V0⋅ρ=V⋅ρ−m
Thus,
V0=V⋅ρ−mρ
Since the sphere is floating half immersed, we know that:
m=V2⋅ρ
Substituting this into the equation for V0:
V0=V⋅ρ−V2⋅ρρ=V⋅ρ−V2⋅ρρ=V2
Therefore, the minimum volume of water that needs to be poured inside the sphere for it to sink completely is:
V0=V2
The minimum volume of water that needs to be poured inside the sphere is V2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct21videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Comprehension32videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If a sphere of radius 3 is inscribed in a cube such that it is tangent to all six faces of the cube, the volume contained outside the sphere and inside the cube is
A97B103C109D115 - Question 2 - Select One
The ratio of the surface area of sphere A to the surface area of sphere B is 729 : 1. What is ratio of the volume of sphere A to sphere B ?
A27:1B81:1C19,683:1D26,224:1
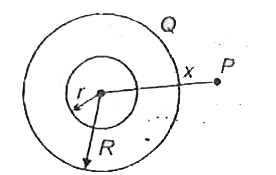
Two concentric hollow conducting spheres of radius r and R are shown. The charge on outer shell is Q. what charge should be given to inner sphere so that the potential at any point P outside the outer sphere is zero ?
 View Solution
View SolutionA small hollow sphere having a small hole in it is immersed in water to a depth of 50cm, before any water penetrates into it. Calculate the radius of the hole, if the surface tension of water is 7.2×10−2Nm−1.
View SolutionA cylindrical can, whose base is horizontal and of radius 3-5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
the total surface area of the can in contact with water when the sphere is in it,View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
View SolutionA cylindrical can, whose base is horizontal and of radius 3-5 cm, contains sufficient water so that when a sphere is placed in the can, the water just covers the sphere. Given that the sphere just fits into the can, calculate :
the depth of water in the can before the sphere was put into the can.View SolutionA hollow spherical body of inner and outer radii 6 cm, and 8 cm respectively floats half submerged in water. Find the density of the material of the sphere.
View Solution

