Question

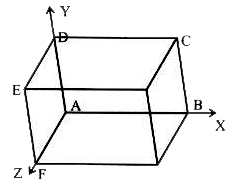
A loop made of straight edegs has six corners at $A(0,0,0),B(L,O,0)C(L,L,0),D(0,L,0)E(0,L,L)$ and $F(0,0,L)$. Where $L$ is in meter. A magnetic field $B=B_0(\hat{i}+\hat{k})T$ is present in the region. The flux passing through the loop $ABCDEFA$ (in that order) is

Options

A. `B_(0)L^(2)Wb`
B. `2B_(0)L^(2)Wb`
C. `sqrt2B_(0)L^(2)Wb`
D. `4B_(0)L^(2)Wb`

Answer

B

Explanation

To solve the problem of calculating the magnetic flux through the loop ABCDEFA, we will follow these steps:

Step 1: Identify the coordinates of the points
The loop is defined by the points:
- A(0, 0, 0)
- B(L, 0, 0)
- C(L, L, 0)
- D(0, L, 0)
- E(0, L, L)
- F(0, 0, L)

Step 2: Determine the area of the loop
The loop consists of two rectangular areas:
1. The area ABCD lies in the XY-plane.
2. The area AEF lies in the YZ-plane.

The dimensions of both rectangles are L x L.

- Area of rectangle ABCD (A1) = L * L = L²
- Area of rectangle AEF (A2) = L * L = L²

Step 3: Define the area vectors
The area vector for each rectangle is defined as follows:
- For area ABCD (A1), the area vector is directed along the Z-axis:
\( \vec{A_1} = L^2 \hat{k} \)

- For area AEF (A2), the area vector is directed along the Y-axis:
\( \vec{A_2} = L^2 \hat{j} \)

Step 4: Define the magnetic field
The magnetic field is given as:
\( \vec{B} = B_0 (\hat{i} + \hat{k}) \)

Step 5: Calculate the magnetic flux through each area
The magnetic flux (\(\Phi\)) through a surface is given by the dot product of the magnetic field and the area vector:
\( \Phi = \vec{B} \cdot \vec{A} \)

For area ABCD (A1):
\( \Phi_1 = \vec{B} \cdot \vec{A_1} = B_0 (\hat{i} + \hat{k}) \cdot (L^2 \hat{k}) = B_0 L^2 (\hat{k} \cdot \hat{k}) = B_0 L^2 \)

For area AEF (A2):
\( \Phi_2 = \vec{B} \cdot \vec{A_2} = B_0 (\hat{i} + \hat{k}) \cdot (L^2 \hat{j}) = B_0 L^2 (\hat{i} \cdot \hat{j} + \hat{k} \cdot \hat{j}) = 0 \)
(Since \(\hat{i} \cdot \hat{j} = 0\) and \(\hat{k} \cdot \hat{j} = 0\))

Step 6: Calculate the total magnetic flux
The total magnetic flux through the loop ABCDEFA is the sum of the fluxes through the two areas:
\( \Phi_{total} = \Phi_1 + \Phi_2 = B_0 L^2 + 0 = B_0 L^2 \)

Step 7: Final answer
The total magnetic flux passing through the loop ABCDEFA is:
\( \Phi_{total} = B_0 L^2 \)