A metal rod OA of mann 'm' and length 'r' is kept rotating with a constantangular speed ω in a vertical plane about a horizontal axis at the end O. The free end A is arraged to slide without friction along fixed conduction circular ring in the same plane as that of rotation. A uniform and constant magnetic induction →B is applied perpendicular and into the plane of rotation as shown in the figure below. An inductor L and an external resistance R are connected through a swithch S between the point O and a point C on the ring to form an electrical circuit. Neglect the resistance of the ring and the rod. Initially, the switch is open.
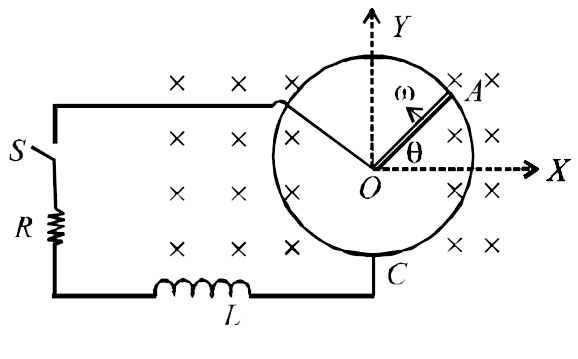
(a) What is the induced emf across the teminal of the switch?
(b) The switch S is closed at time t=0.
(i) Obtain an expression for the current as a function of time.
(ii) In the steady state, obtin the time dependence of the torque required to maintain the constant angular speed, given that the rod OA was along th positive X-axis at t=0.
The correct Answer is:A, B, C, D
(a) Let us consider a small length of metal rod dx at a distance x from the origin. Small amount of emf (de) induced in this small length (due to metallic rod cutting megnetic lines of force) is
de=B(dx)v ...(i)
where v is the velocity of small length dx
v=x(Ω) ...(ii)
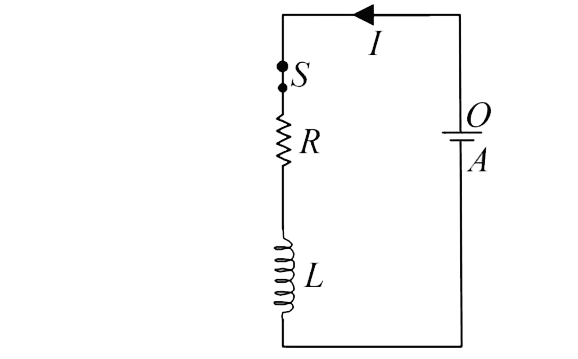
∴Totalemfacrossthewho≤mηllicrodOAis<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_EIA_C15_043_S01.pngwh=80%mx-autosty≤=background:white;><br>e=int_(0)^(r) Bx(omega)dx=B(omega)[(x^20/(2)]_(0)^(r)=(Br^(2)omega)/(2)<br>(b)Theabovediagramcanbereconstrucedastheadjacentfigure,eisaconstant.Owillauμlatepostivechar≥andA¬ative.WhentheswitchSisclosed,transientcurrentatanytimet,whencurrentIisflow∈g∈the∘uit,<br>I=(I_0)(1-e^(t//tau))<br>Here,<br>(I_0)=e/R =( B omegar^2)/(2R)<br>and(tau)=L/R<br>Therefore,I=Bωr22R[1−e−RLt)]
(ii) In steady state,
I=Bωr22R[∴thasalar≥valueande−(RT)t→0]
When current flows in the circuit in steady state, there is a power loss through the resistor,
Also since the rid ritating in a vertical planem work needs Power loss due to current I will be
P=(I2)R=(Br2ω2R)2R
If torque required for this Power
is (τ1) then
P=(τ1)(ω)
⇒(τ1)=B2r4ω4R
Torque required to move the rod in circular motion against gravitational field
(τ2)=mg×r2cos(θ)
The totla torque
(τ)=(τ1)+(τ2) (clockwise).
(τ)=b2r2ω4R+mgr2cosωt
The required torque will be of same magnitude and in anticlockwise direction. The second term will change signs as the value of cos(θ) can be positive as well as negative.
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
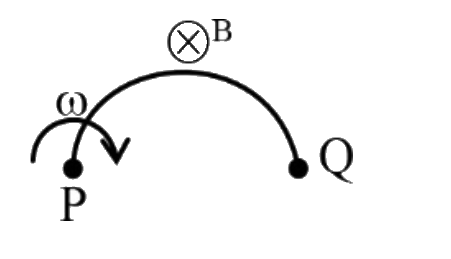
View SolutionA conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
When a rod of length l is rotated with angular velocity of ω in a perpendicular field of induction B , about one end , the emf across its ends is
ABl2ωBBl2ω2CBlωDBlω2 - Question 2 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 3 - Select One

A uniform rod of legth L is free to rotate in a vertica plane about a fixed horizontal axis through B. The rod begins rotating from rest. The angular velocity ω at angle θ is given asA√(6gL)sin(θ2)B√(6gL)cos(θ2)C√(6gL)sinθD√(6gL)cosθ
A thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA wire is bent to form a semicircle of the radius a. The wire rotates about its one end with angular velocity ω . Axis of rotation is perpendicular to the plane of the semicircle . In the space , a uniform magnetic field of induction B exists along the aixs of rotation as shown in the figure . Then -
 View Solution
View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.View SolutionA conducting rod AB moves parallel to x-axis in a uniform magnetic field pointing perpendicular and into the plane of paper. The end A of the rod
 View Solution
View SolutionA conducting rod of length 2l is rotating with constant angular speed ω about is perpendicular bisector. A uniform magnetic field →B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
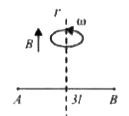 View Solution
View Solution

