A narrow slit S transmitting light of wavelength λ is placed a distance d above a large plane mirror as shown in figure. The light coming directly from the slit and that coming after the reflection interference at a screen ∑ placed at a distance LD from the slit. a. What will be the intensity at a point just above the mirror. i.e., just above O? b. At what distance from O does the first maximum occur?
?
The correct Answer is:A, B, D
a. Since there is a phase difference of π between direct light and reflecting light the intensity just above the mirror will be zero.ltbr> B. Here 2nd= equivalent slit seperationn
D=distance between slit and screen.
We know for bright fringe
△x=y×2dD=nλ
But as thereis a phase reversal of λ2
→(y×2d)D=λ2=nλ
→y×2dD=nλ=λ2(n−12)=λ2
→y=λD4D
Topper's Solved these Questions
Similar Questions
A long narrow horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and that after reflection is seen on a screen 1.0 in away from the slit, Find the fringe-width if the light used has a wavelength of 700 nm.
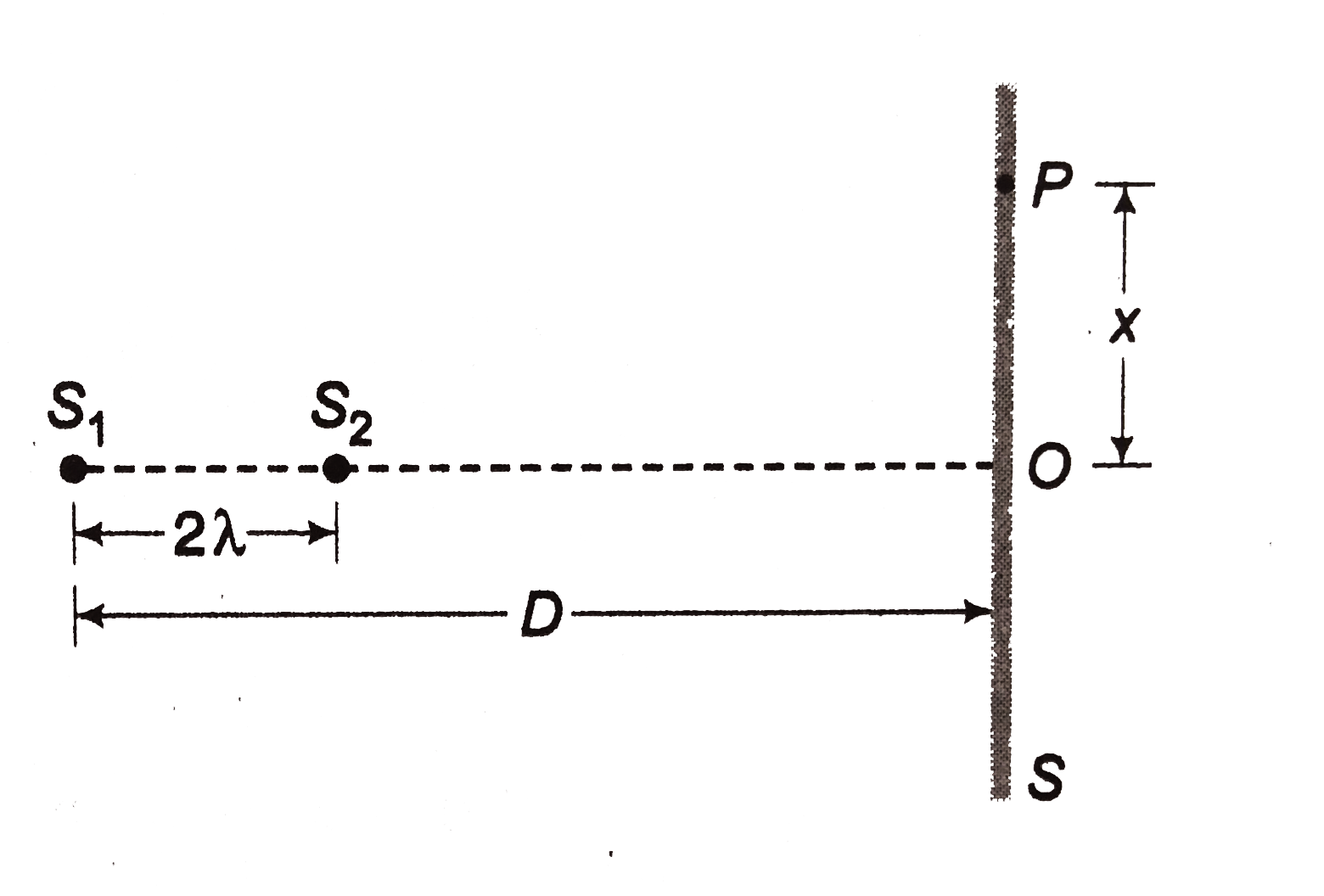
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
 .
.
View Solution
Knowledge Check
In a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.
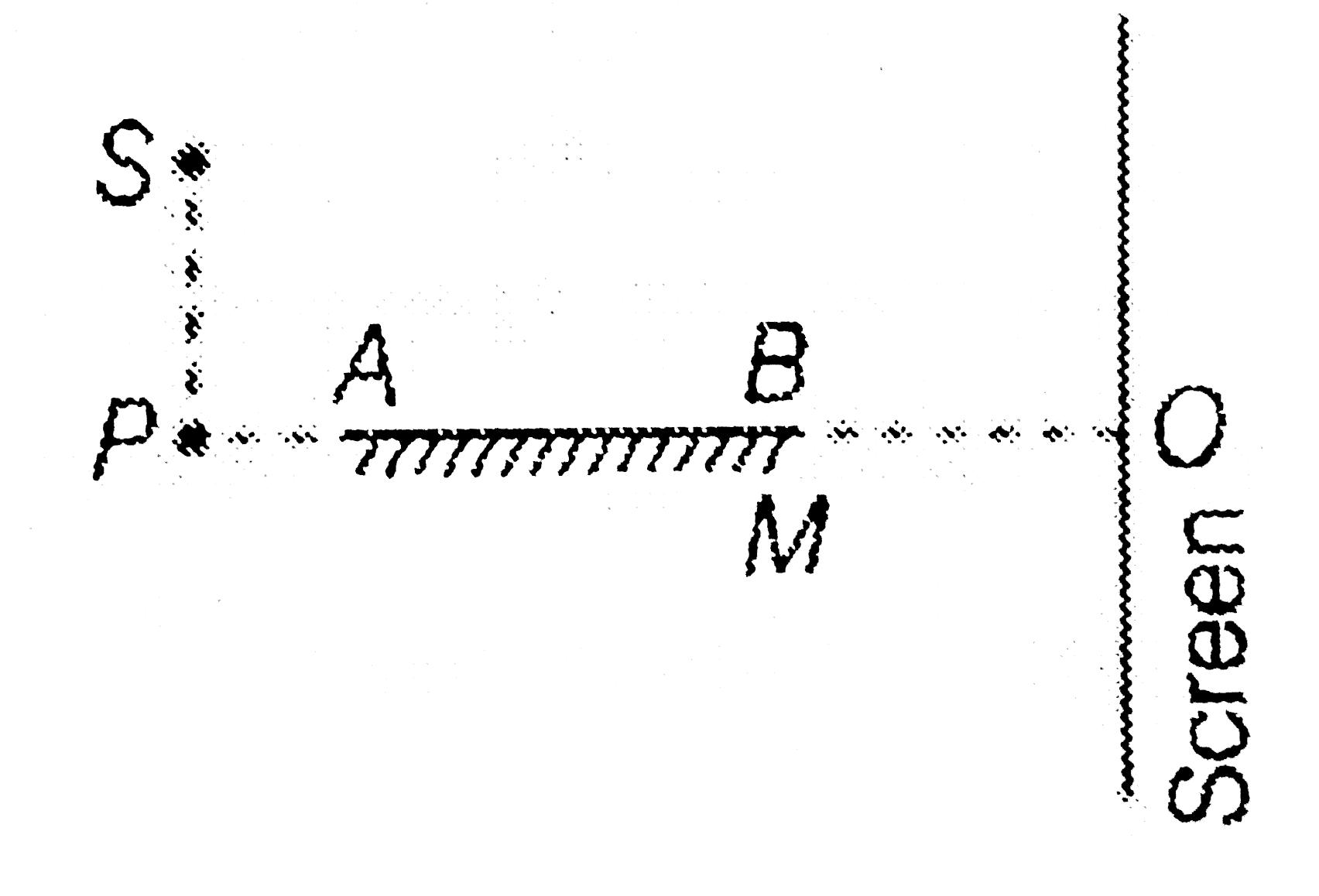
If the mirror is shifted towards left then how does the fringe pattern on screen changes ?Afringe width decreases and the region in which interference is formed shifts downwardsBfringe width decreases and the region in which interference is formed shifts upwardsCfringe width does not change and the region in which interference is formed shifts upwardsDfringe width does not change and the region in which interference is formed shifts downwardsIn a Lloyds's mirror experiment as narraow slit S iransmitting a light of wavelength λ is placed 3 mm above a small plane mirror ( as shown). The light coming directly from the the slit and that coming after the reflection interfere on a screen placed at a distance of 90 cm from the slit. Length of mirror is 2 mm and the middle point of mirror is 2 mm from point P.

If fringe width is 0.1 mm then what is the wavelength of light used ?A3.33×10−7mB6.67×10−7mC1.0×10−7mD4×10sA long horizontal slit is placed 1 mm above a horizontal plane mirror. The interference between the light coming directly from the slit and the after reflection is seen on a screen 1 m away from the slit. If the mirror reflects only 64% of the light falling on it, the ratio of the maximum to the minimum intensity in the interference pattern observed on the screen is
A8:1B3:1C81:1D9:1
_E01_037_Q01.png)
Two coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 3λ the light is collected on a screen S which is placed at a distance D(>>λ) from the slits the smallest distance x such that the P is a maxima.
View SolutionA point is emitting light of wavelength 6000Å is placed at a very small height h above a flat reflecting surface MN as shown in the figure.The intensity of the reflected light is 36% of the incident intensity.Interference fringes are observed on a screen placed parallel to the reflecting surface at a very large distance D from it.

If the intensity at pbe maximum then the minimum distance through which the reflecting suface MN should be displaced so that at P again becomes a mixture.?
View SolutionA long narrow horizontal slit lies 1mm above a plane mirror. The interference pattern produced by the slit and its and its image is viewed on a screen ∑ distance 1m from the slit. The wavelength of light is 600nm. Then the distance of the first maxima above the mirror is equal to (d<<D) :

View SolutionLight d of wavelength 5000Å is incident normally on a slite. The first minimum of the distance of 5 mm from the central maximum on a screen placed at a distance of 2 m from the slit. The width of slit is
View SolutionLight of wavelength λ is incident on a slit. First minima of the diffraction pattern is found to lie at a distance of 6 mm from the central maximum on a screen placed at a distance of 2 m from the slit. If slit width is 0.2 mm, then wavelength of the light used will be :
View Solution
