A particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
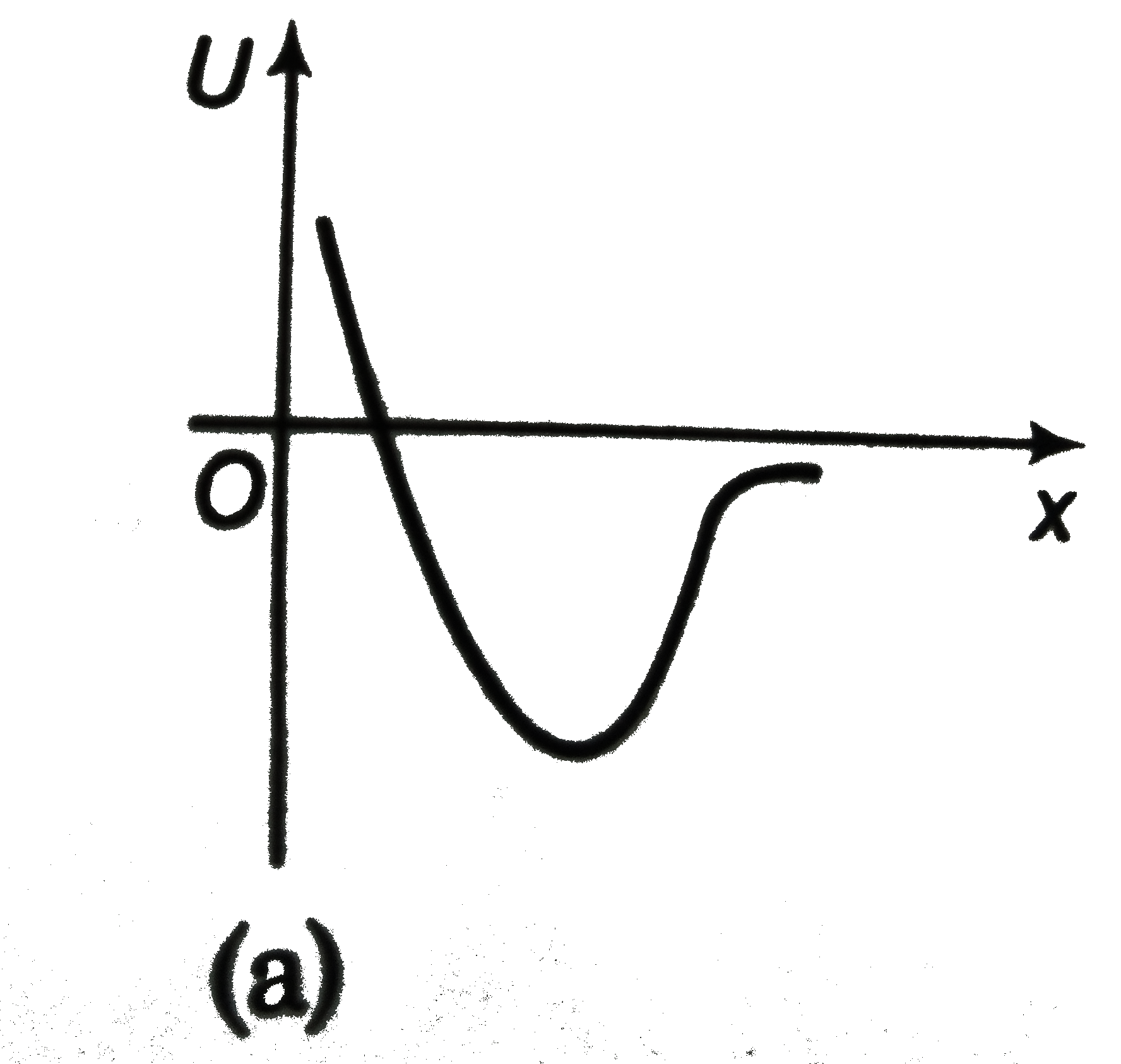
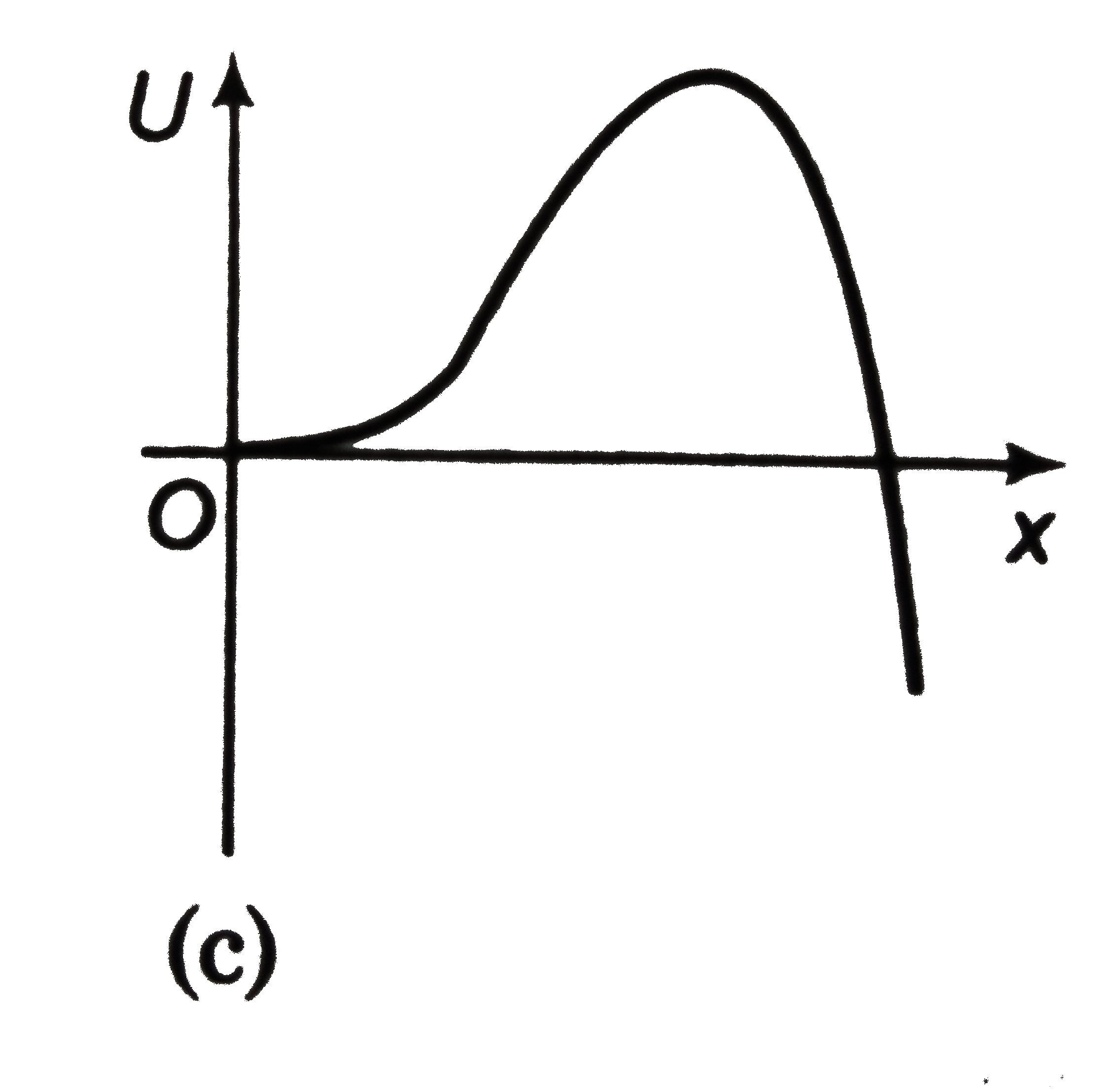
The correct Answer is:C
To solve the problem, we need to find the potential energy function U(x) corresponding to the given force F(x)=−ax+bx2. The relationship between force and potential energy is given by:
F=−dUdx
Step 1: Write the expression for potential energy
From the relationship above, we can express the change in potential energy as:
dU=−Fdx
Substituting the expression for F:
dU=−(−ax+bx2)dx=(ax−bx2)dx
Step 2: Integrate to find U(x)
Now, we integrate to find the total potential energy U(x):
U(x)=∫(ax−bx2)dx
Calculating the integral:
U(x)=∫axdx−∫bx2dx
U(x)=a2x2−b3x3+C
Where C is the constant of integration.
Step 3: Determine the points where U(x)=0
To find the points where the potential energy is zero, we set U(x)=0:
a2x2−b3x3+C=0
Assuming C=0 for simplicity (we can choose the reference point for potential energy), we have:
a2x2−b3x3=0
Factoring out x2:
x2(a2−b3x)=0
This gives us two solutions:
1. x=0
2. a2−b3x=0 which leads to x=3a2b
Step 4: Analyze the behavior of U(x)
- At x=0, U(0)=0.
- As x increases from 0, the term a2x2 dominates initially, making U(x) positive.
- As x continues to increase, the −b3x3 term will eventually dominate, causing U(x) to decrease and become negative after reaching a maximum.
Step 5: Determine the correct graph
Given the behavior of U(x):
- It starts at 0 when x=0.
- It increases to a maximum and then decreases, eventually becoming negative.
Thus, the correct representation of the potential energy function U(x) is best represented by option C, which shows the potential energy starting at zero, increasing, reaching a maximum, and then decreasing through zero into negative values.
Summary of Steps:
1. Write the expression for potential energy using the force.
2. Integrate to find the potential energy function.
3. Set the potential energy function to zero to find critical points.
4. Analyze the behavior of the potential energy function.
5. Identify the correct graph representation.
From the relationship above, we can express the change in potential energy as:
Now, we integrate to find the total potential energy U(x):
To find the points where the potential energy is zero, we set U(x)=0:
2. a2−b3x=0 which leads to x=3a2b
- At x=0, U(0)=0.
- As x increases from 0, the term a2x2 dominates initially, making U(x) positive.
- As x continues to increase, the −b3x3 term will eventually dominate, causing U(x) to decrease and become negative after reaching a maximum.
Given the behavior of U(x):
- It starts at 0 when x=0.
- It increases to a maximum and then decreases, eventually becoming negative.
1. Write the expression for potential energy using the force.
2. Integrate to find the potential energy function.
3. Set the potential energy function to zero to find critical points.
4. Analyze the behavior of the potential energy function.
5. Identify the correct graph representation.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective
15 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
On a particle placed at origin a variable force F=−ax(where a is a positive constant) is applied. If U(0)=0, the graph between potential energy of particle U(x) and x is best represented by:-
View SolutionA particle of mass m moving along x-axis has a potential energy U(x)=a+bx2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionA particle of mass m moving along x-axis has a potential energy U(x)=a+bx2 where a and b are positive constant. It will execute simple harmonic motion with a frequency determined by the value of
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the particle is.
(a)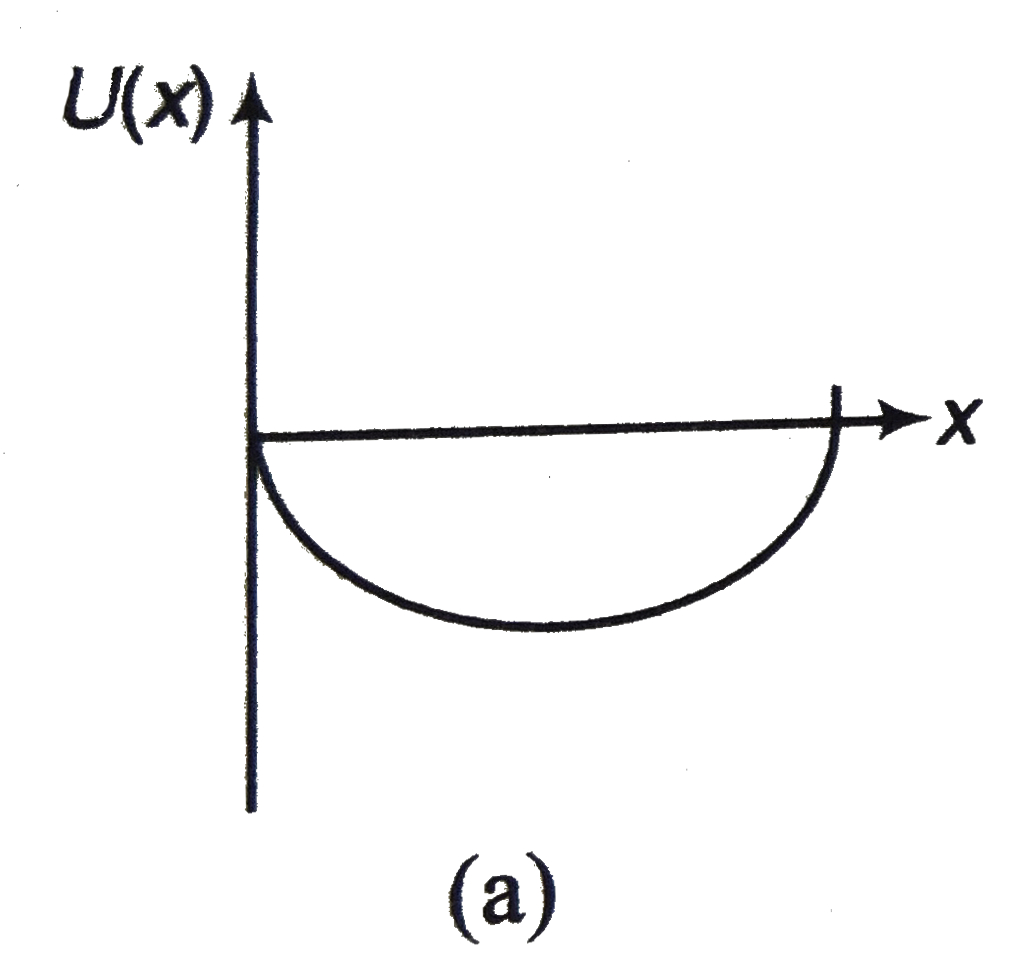 , (b)
, (b) 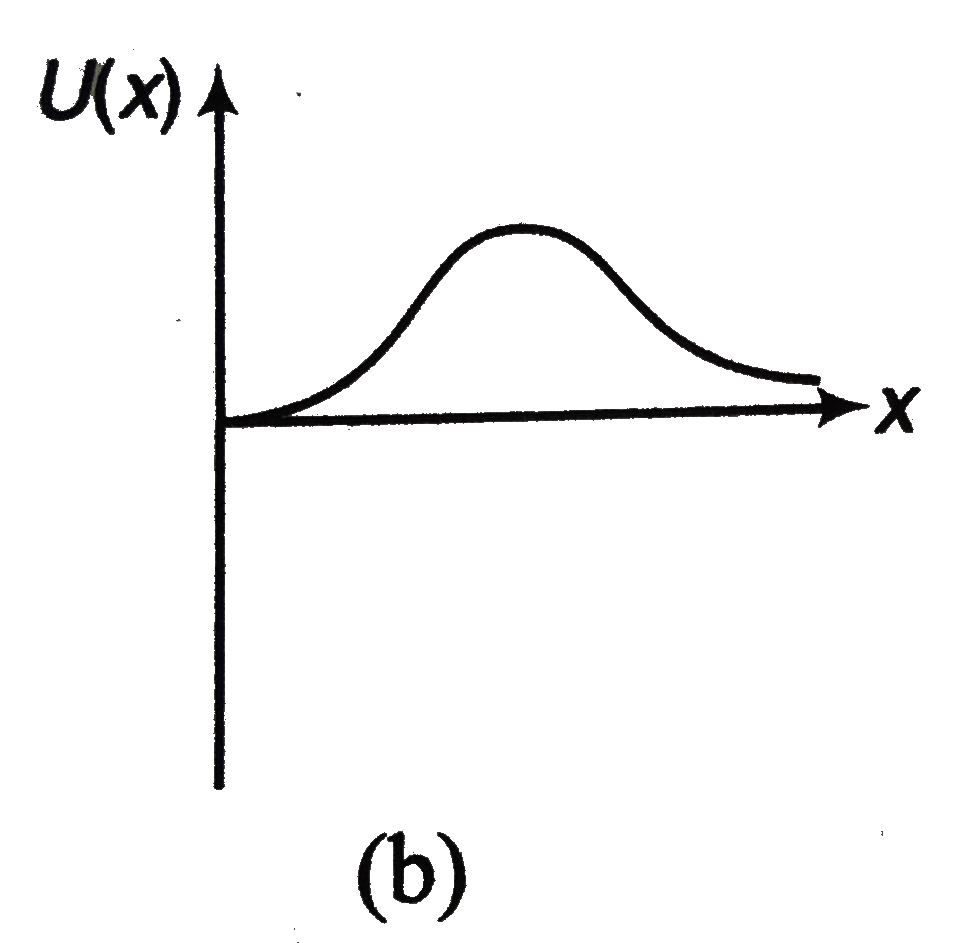 , (c)
, (c) 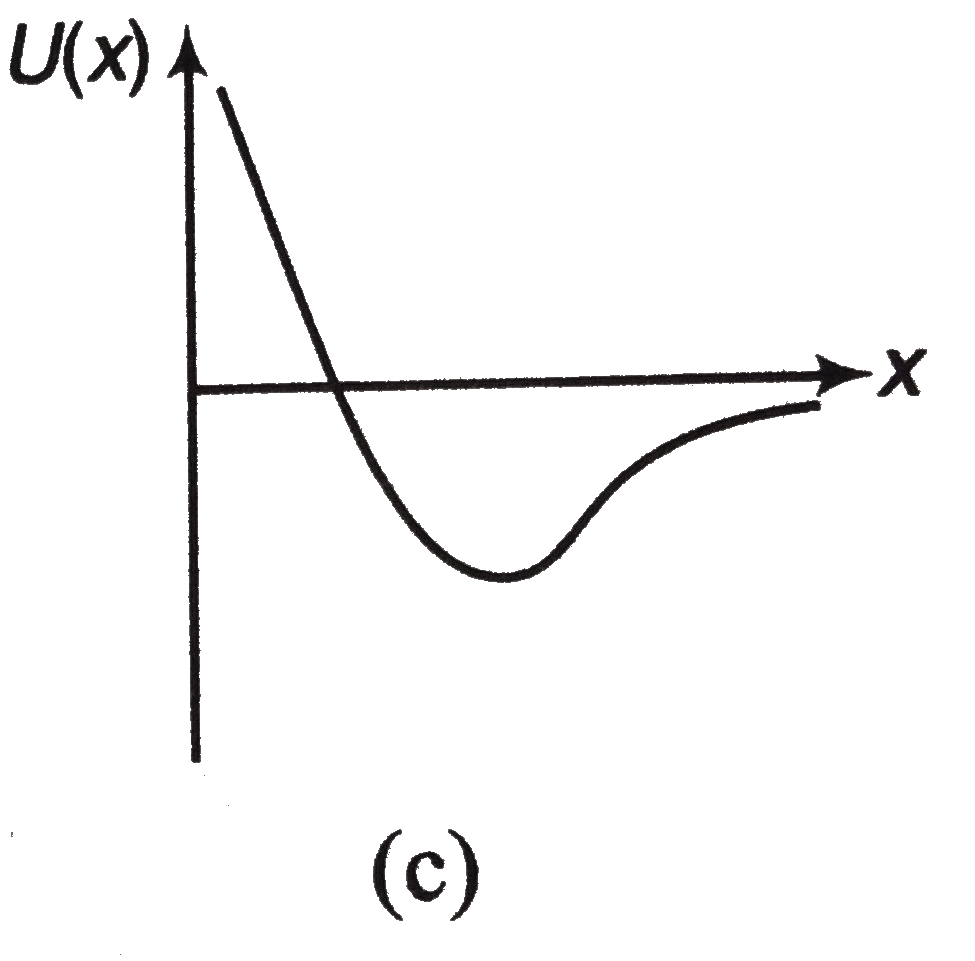 , (d)
, (d) 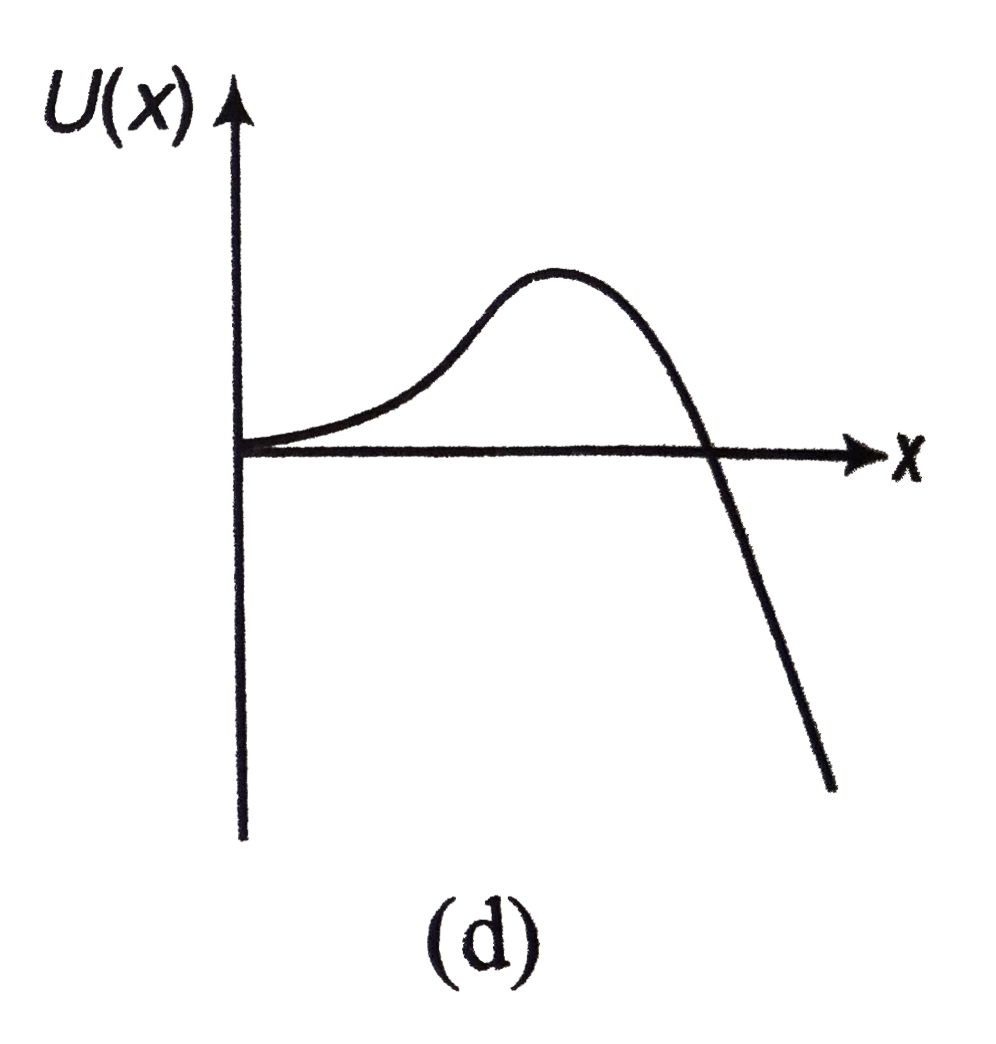 .
.
View SolutionA particle moving along the x axis is acted upon by a single force F = F0e−kx , where F0 and k are constants. The particle is released from rest at x = 0. It will attain a maximum kinetic energy of :
View SolutionA particle of mass m moves in a one dimensional potential energy U(x)=−ax2+bx4, where a and b are positive constant. The angular frequency of small oscillation about the minima of the potential energy is equal to
View SolutionA particle is acted by x force F=Kx where K is a(+ve) constant its potential energy at x=0 is zero . Which curve correctly represent the variation of potential energy of the block with respect to x
View SolutionTwo identical positive charges are placed at x=−a and x=a. The correct variation of potential V along the x-axis is given by
View SolutionFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View Solution