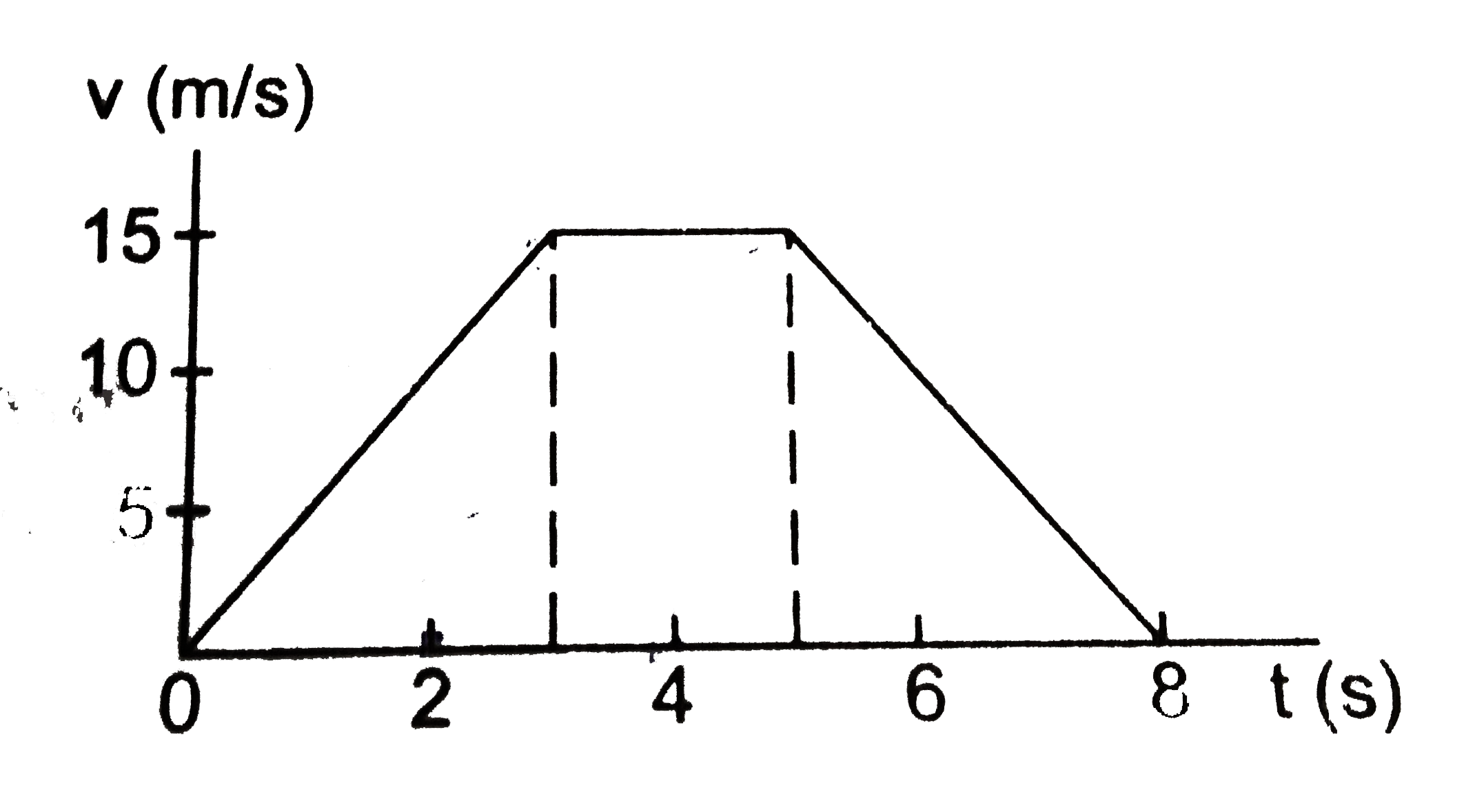
A particle of mass 1 g moves on a straight line. The variation of its velocity with time is shown in fig. Find the force acting on the particle att = 1 s,4s and 7 s.
To solve the problem, we need to determine the force acting on a particle of mass 1 g (which is 0.001 kg) at three different times: t = 1 s, t = 4 s, and t = 7 s. The force can be calculated using Newton's second law, F=ma, where a is the acceleration of the particle.
Step 1: Find the acceleration at t = 1 s
- From the velocity-time graph, we can determine the acceleration by finding the slope of the line between t = 0 s and t = 3 s.
- The initial velocity vi=0 m/s (at t = 0 s) and the final velocity vf=15 m/s (at t = 3 s).
- The time interval Δt=3−0=3 s.
Using the formula for acceleration:
a=vf−viΔt=15−03−0=153=5m/s2
Step 2: Calculate the force at t = 1 s
- Now we can find the force using F=ma:
F=(0.001kg)(5m/s2)=0.005N=5×10−3N
Step 3: Find the acceleration at t = 4 s
- For t = 4 s, we look at the segment of the graph from t = 3 s to t = 5 s.
- The initial velocity at t = 3 s is vi=15 m/s and the final velocity at t = 5 s is vf=5 m/s.
- The time interval Δt=5−3=2 s.
Calculating the acceleration:
a=vf−viΔt=5−152=−102=−5m/s2
Step 4: Calculate the force at t = 4 s
- Using F=ma:
F=(0.001kg)(−5m/s2)=−0.005N=−5×10−3N
Step 5: Find the acceleration at t = 7 s
- For t = 7 s, we analyze the segment from t = 5 s to t = 8 s.
- The initial velocity at t = 5 s is vi=5 m/s and the final velocity at t = 8 s is vf=0 m/s.
- The time interval Δt=8−5=3 s.
Calculating the acceleration:
a=vf−viΔt=0−53=−53≈−1.67m/s2
Step 6: Calculate the force at t = 7 s
- Using F=ma:
F=(0.001kg)(−1.67m/s2)≈−0.00167N=−1.67×10−3N
Summary of Forces
- At t=1s: F=5×10−3N
- At t=4s: F=−5×10−3N
- At t=7s: F≈−1.67×10−3N
- From the velocity-time graph, we can determine the acceleration by finding the slope of the line between t = 0 s and t = 3 s.
- The initial velocity vi=0 m/s (at t = 0 s) and the final velocity vf=15 m/s (at t = 3 s).
- The time interval Δt=3−0=3 s.
a=vf−viΔt=15−03−0=153=5m/s2
- Now we can find the force using F=ma:
F=(0.001kg)(5m/s2)=0.005N=5×10−3N
- For t = 4 s, we look at the segment of the graph from t = 3 s to t = 5 s.
- The initial velocity at t = 3 s is vi=15 m/s and the final velocity at t = 5 s is vf=5 m/s.
- The time interval Δt=5−3=2 s.
a=vf−viΔt=5−152=−102=−5m/s2
- Using F=ma:
F=(0.001kg)(−5m/s2)=−0.005N=−5×10−3N
- For t = 7 s, we analyze the segment from t = 5 s to t = 8 s.
- The initial velocity at t = 5 s is vi=5 m/s and the final velocity at t = 8 s is vf=0 m/s.
- The time interval Δt=8−5=3 s.
a=vf−viΔt=0−53=−53≈−1.67m/s2
- Using F=ma:
F=(0.001kg)(−1.67m/s2)≈−0.00167N=−1.67×10−3N
- At t=1s: F=5×10−3N
- At t=4s: F=−5×10−3N
- At t=7s: F≈−1.67×10−3N
Similar Questions
A paticle of mass 50 g moves on a straight line. The vatiation of speed with time is shown in figure. Find the force acting on the particle at t=2,4 and 6 secons.
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionKinetic energy of a particle moving in a straight line is proportional to the time t. The magnitude of the force acting on the particle is :
View SolutionA particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionA particle is moving on a straight line x + y = 2. Its angular momentum about origin is L = 3t + 2 (kg m2s−1). Find the force acting on the particle at t = 2 s. (x and y are in metre)
View SolutionPower of the only force acting on a particle of mass m=1 kg moving in straight line depends on its velocity as P=v2 where v is in m/s and P is in watt. If initial velocity of the particle is 1m/s, then the displacement of the particle in ln2 second will be :
View SolutionA particle starts motion from rest and moves along a straight line. Its velocity-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionKinetic energy of a particle moving in a straight line varies with time t as K=4t2. The force acting on the particle
View SolutionA particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA particle of mass 1 kg is moved under the action of a force and velocity time graph of the particle is shown in figure.Work done by the force from t=0 to t=6 s Is
View Solution
