A particle of mass 2kg starts moving in a straight line with an initial velocity of 2m/s at a constant acceleration of 2m/s2. Then rate of change of kinetic energy.
is four times the velocity at any moment
is two times the displacement at any moment
is four times the rate of change of velocity at any moment
is constant throughout
The correct Answer is:A
To solve the problem of finding the rate of change of kinetic energy for a particle with given mass, initial velocity, and constant acceleration, we can follow these steps:
1. Identify Given Values:
- Mass of the particle, m=2kg
- Initial velocity, u=2m/s
- Constant acceleration, a=2m/s2
2. Determine the Velocity at Any Time t:
Using the kinematic equation:
V=u+at
Substitute the known values:
V=2+2t
3. Calculate the Kinetic Energy K:
The formula for kinetic energy is:
K=12mv2
Substitute m and V:
K=12×2×(2+2t)2
Simplifying this:
K=1×(2+2t)2
Expanding (2+2t)2:
K=(22+2⋅2⋅2t+(2t)2)=4+8t+4t2
4. Differentiate Kinetic Energy with Respect to Time t:
We need to find dKdt:
dKdt=ddt(4+8t+4t2)
Differentiating term by term:
dKdt=0+8+8t
Thus,
dKdt=8+8t
5. Express the Result in Terms of Velocity:
We know from our earlier calculation that:
V=2+2t
Therefore, we can express dKdt as:
dKdt=8+8t=4(2+2t)=4V
Final Result:
The rate of change of kinetic energy is:
dKdt=4V
- Mass of the particle, m=2kg
- Initial velocity, u=2m/s
- Constant acceleration, a=2m/s2
Using the kinematic equation:
V=u+at
Substitute the known values:
V=2+2t
The formula for kinetic energy is:
K=12mv2
Substitute m and V:
K=12×2×(2+2t)2
Simplifying this:
K=1×(2+2t)2
Expanding (2+2t)2:
K=(22+2⋅2⋅2t+(2t)2)=4+8t+4t2
We need to find dKdt:
dKdt=ddt(4+8t+4t2)
Differentiating term by term:
dKdt=0+8+8t
Thus,
dKdt=8+8t
We know from our earlier calculation that:
V=2+2t
Therefore, we can express dKdt as:
dKdt=8+8t=4(2+2t)=4V
The rate of change of kinetic energy is:
dKdt=4V
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionA particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
View Solution
Knowledge Check
Acceleration (a)-displacement(s) graph of a particle moving in a straight line is shown here. The initial velocity of the particle is zero. The v-s graph of the particle would be
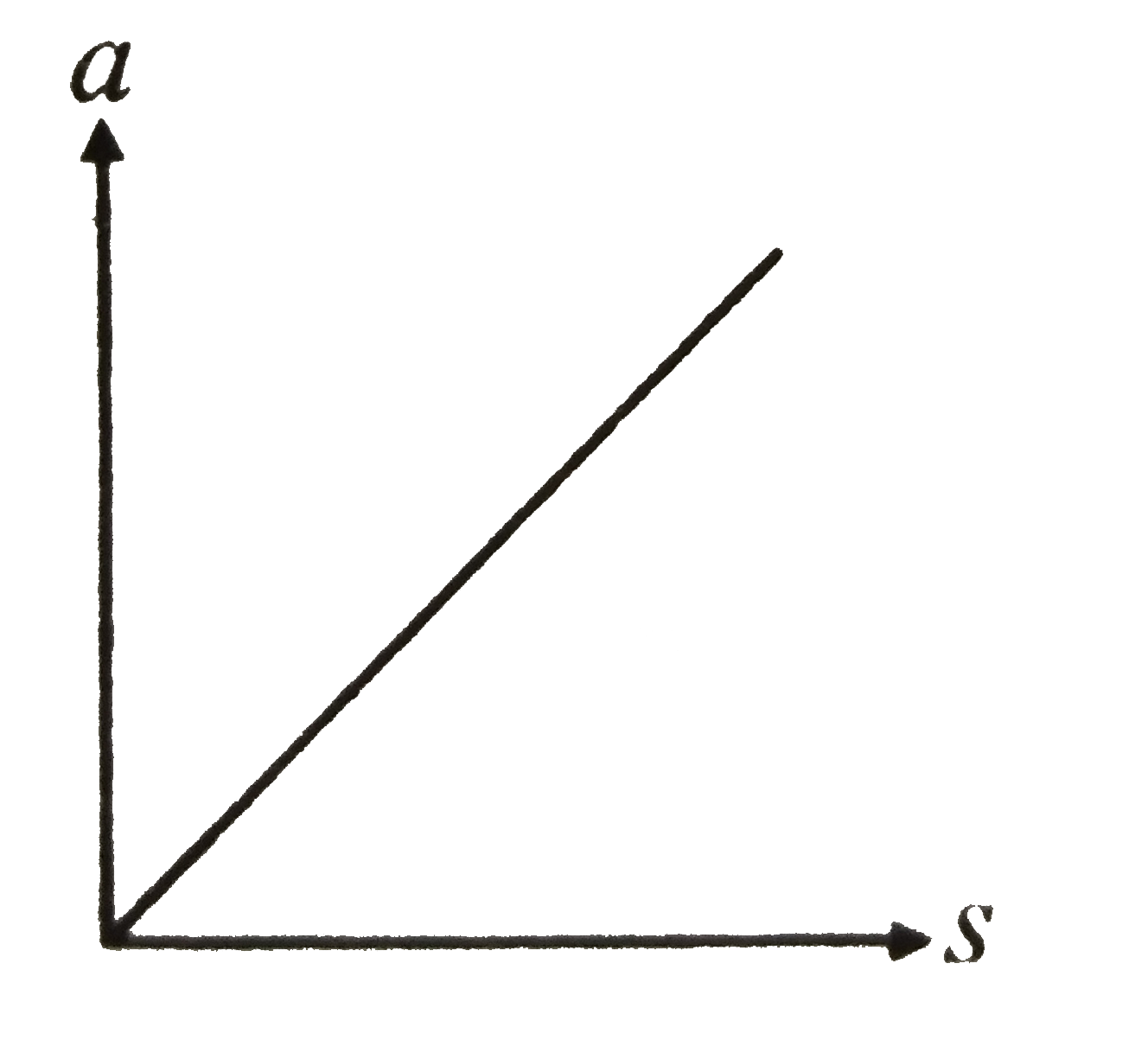 A
A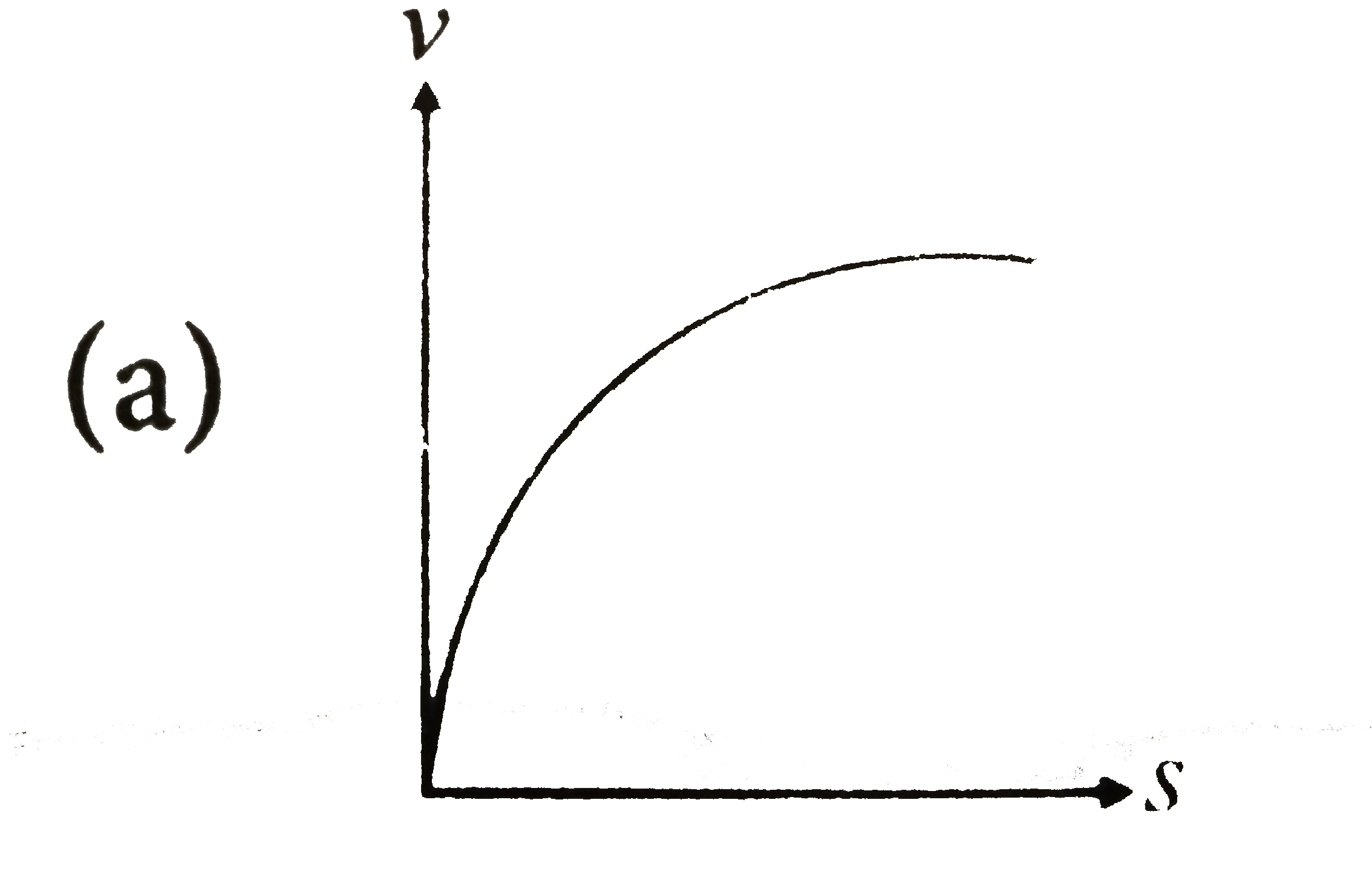 B
B C
C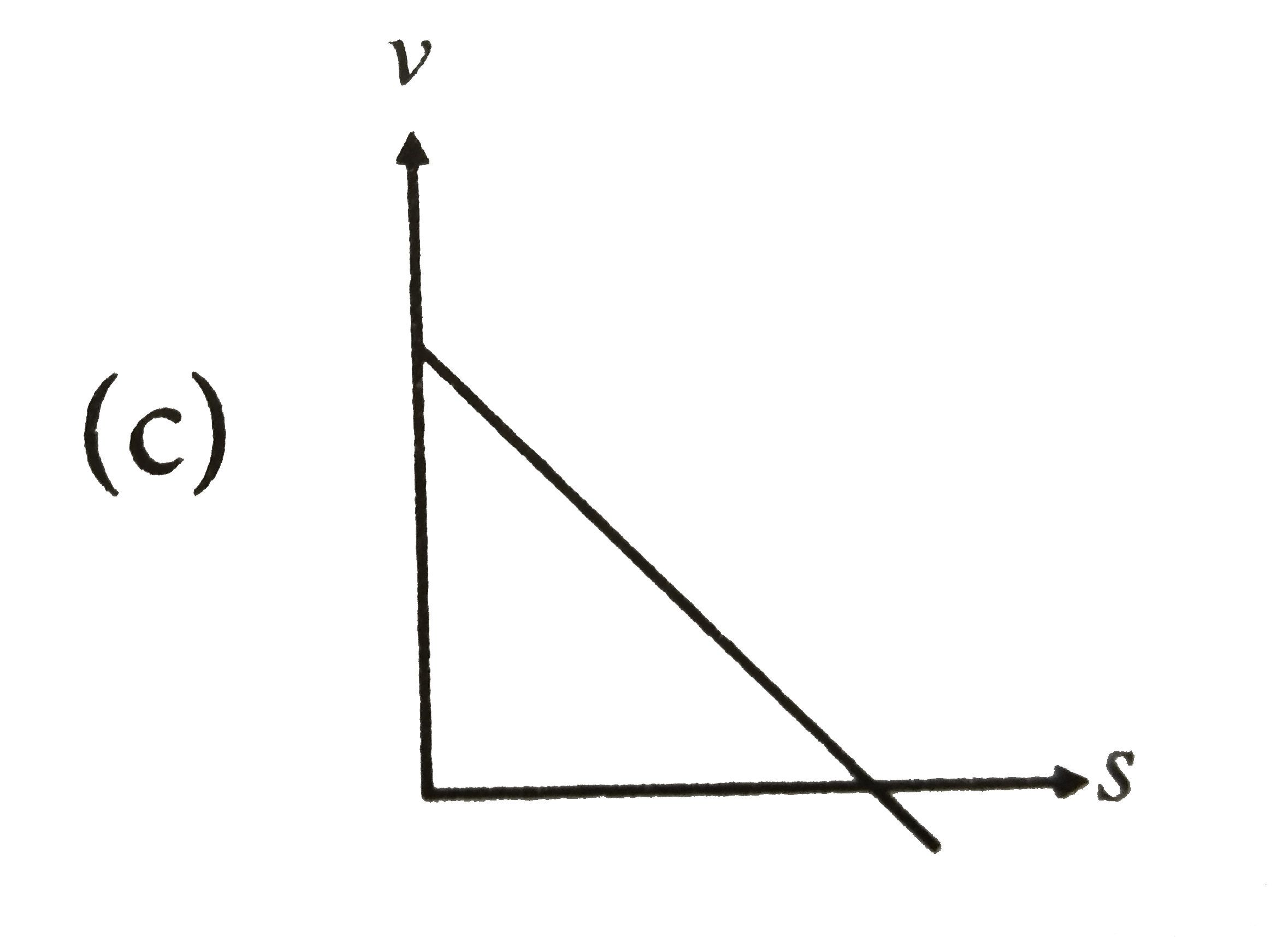 D
D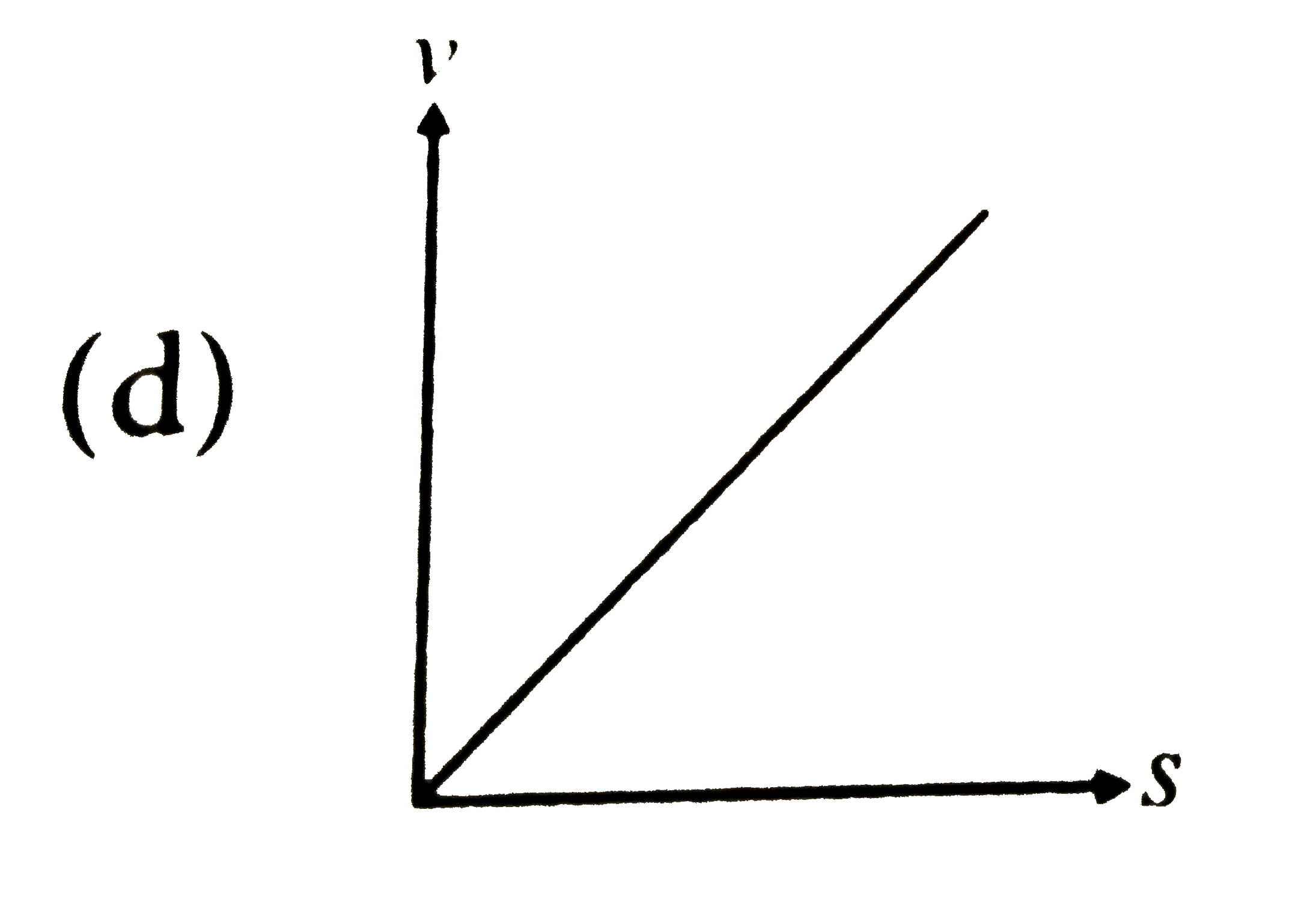
A particle starts to move in a straight line from a point with velocity 10 m s−1 and acceleration - 2.0 ms−2. Find the position and velocity of the particle at (i) t = 5 s, (ii) t' = 10 s.
View SolutionA particle starts from the origin at t = 0 s with a velocity of 10.0ˆj m/s and moves in plane with a constant acceleration of (8ˆi+2ˆj)ms−2. The y-coordinate of the particle in 2 sec is
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA particle has an initial velocity of 9m/s due east and a constant acceleration of 2m/s2 due west. The distance coverd by the particle in the fifth second of its motion is :
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionTwo cars A and B of equal masses (100Kg) are moving on a straight horizontal road with same velocity 3m/s as shown. At t=0 car A starts accelerating with constant acceleration of 2m/s2 (intial separation between car is 25m). Choose correct options (neglect length of cars)

View SolutionAt time t=0, a particle is at (2m,4m). It starts moving towards positive x-axis with constant acceleration 2m/s2 (initial velocity=0). After 2 s, an additional acceleration of 4m/s2 starts acting on the particle in negative y-direction also. Find after next 2 s.
(a) velocity and
(b) coordinates of particle.
View Solution
