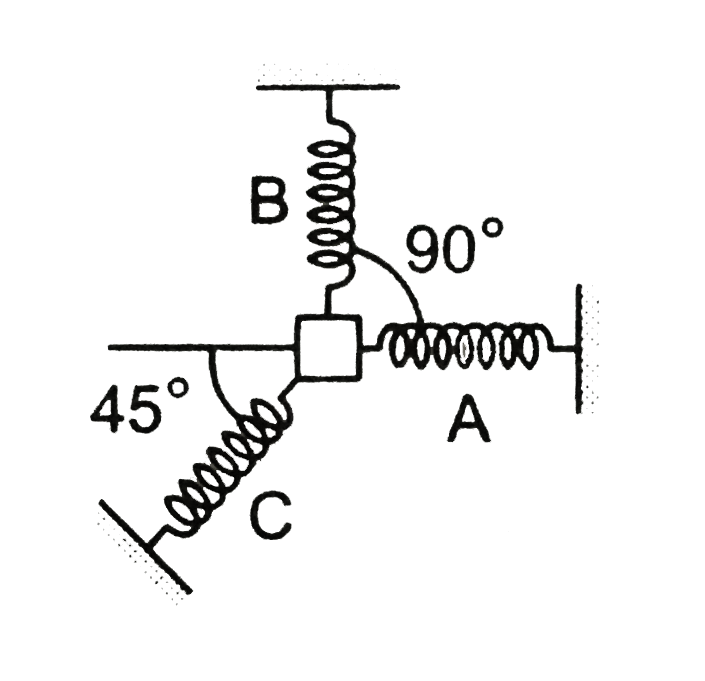
A particle of mass m is asttached to three springs A,B and C of equla force constants k as shown in figure. If the particle is pushed slightly against the spring C and released, find the time period of oscillastion.
The correct Answer is:=2π√m2k
a. Suppose the particle is pushed lightly against the spring C through displacement x.
Total resultat force on the particle ils kx.
Due to spring C and kx2 due to spring A and B.
∴ Total Resultant force
=kx+
⎷(kx)2(√2)2+(kx)2(√2)2
Acceleration =2kxm
Timeperiod=2π√displacement(Acceleration)
=2π√x2kxm
=2π√m2k
[Cause: When the body pushed against C the spring C tries to pulll the block XL. At that moment the spring A and B tries to pull the block with force kx√2andkx√2 respectively towards xy and xz respectively. So the total force on the block is due to the spring force C as well as the component of two spring force A and B.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
2 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A particle of mass m is attached with three springs A,B and C of equal force constancts k as shown in figure. The particle is pushed slightly against the spring C and released. Find the time period of oscillation.
 .
.
View SolutionA block of mass m is attached to three springs A,B and C having force constants k,k and 2k respectively as shown in figure. If the block is slightly oushed against spring C. If the angular frequency of oscillations is √Nkm, then find N. The system is placed on horizontal smooth surface.
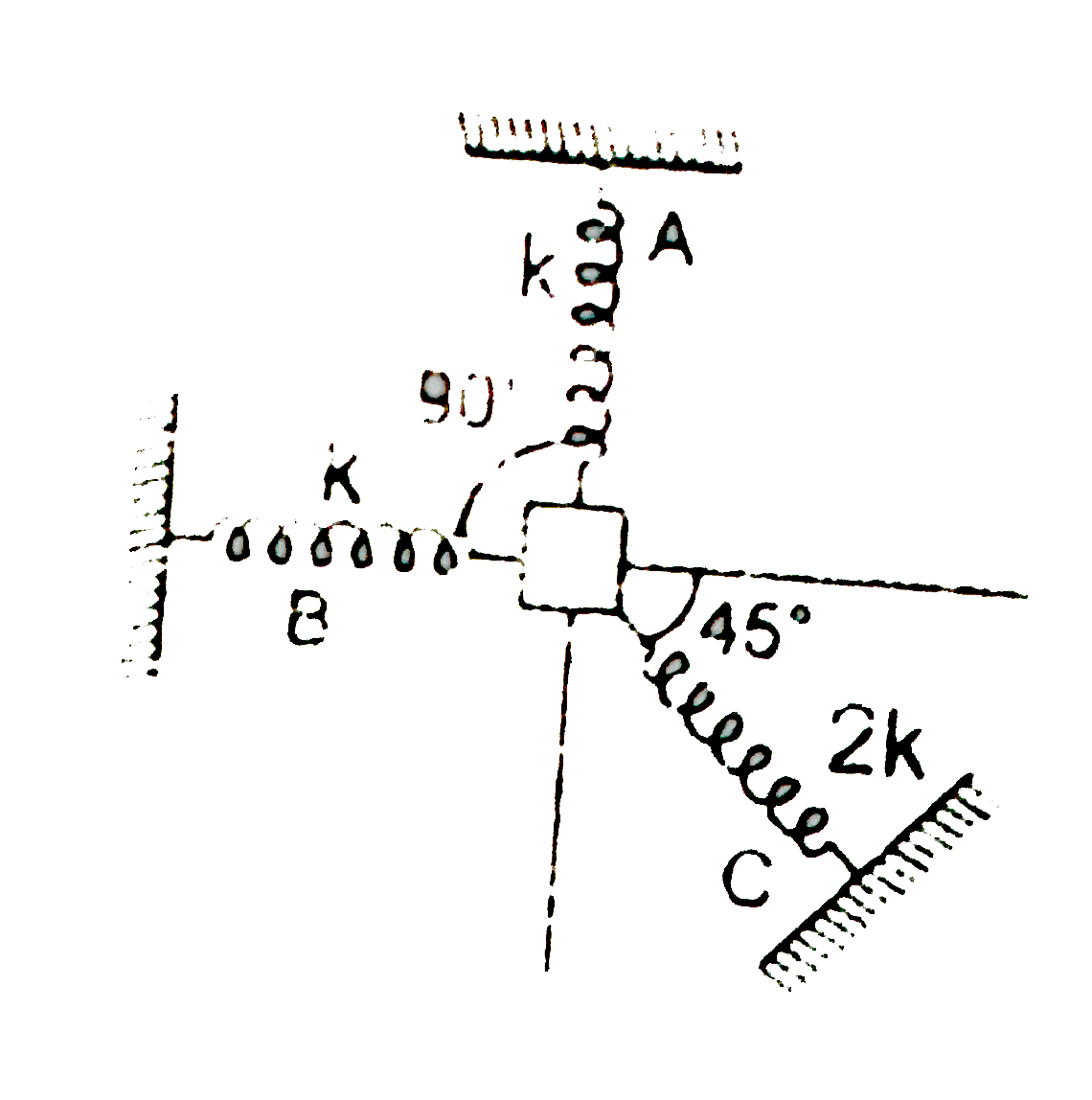
View Solution
Knowledge Check
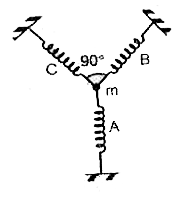
A particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
 AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mK
AT=2π√mKBT=2π√2mKCT=2π√m2KDT=π√mKA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
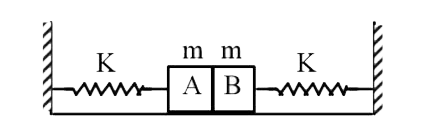
Two blocks each of mass m are connected with springs each of force constant K as shown in fig. The mass A is displaced to the left & B to the right by the same amount and released then the time period of oscillation is -
View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
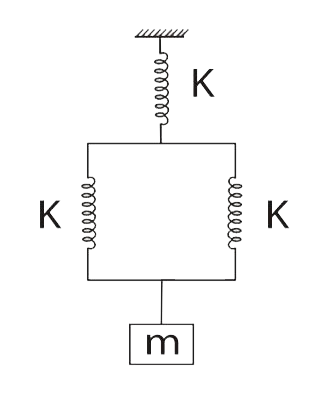
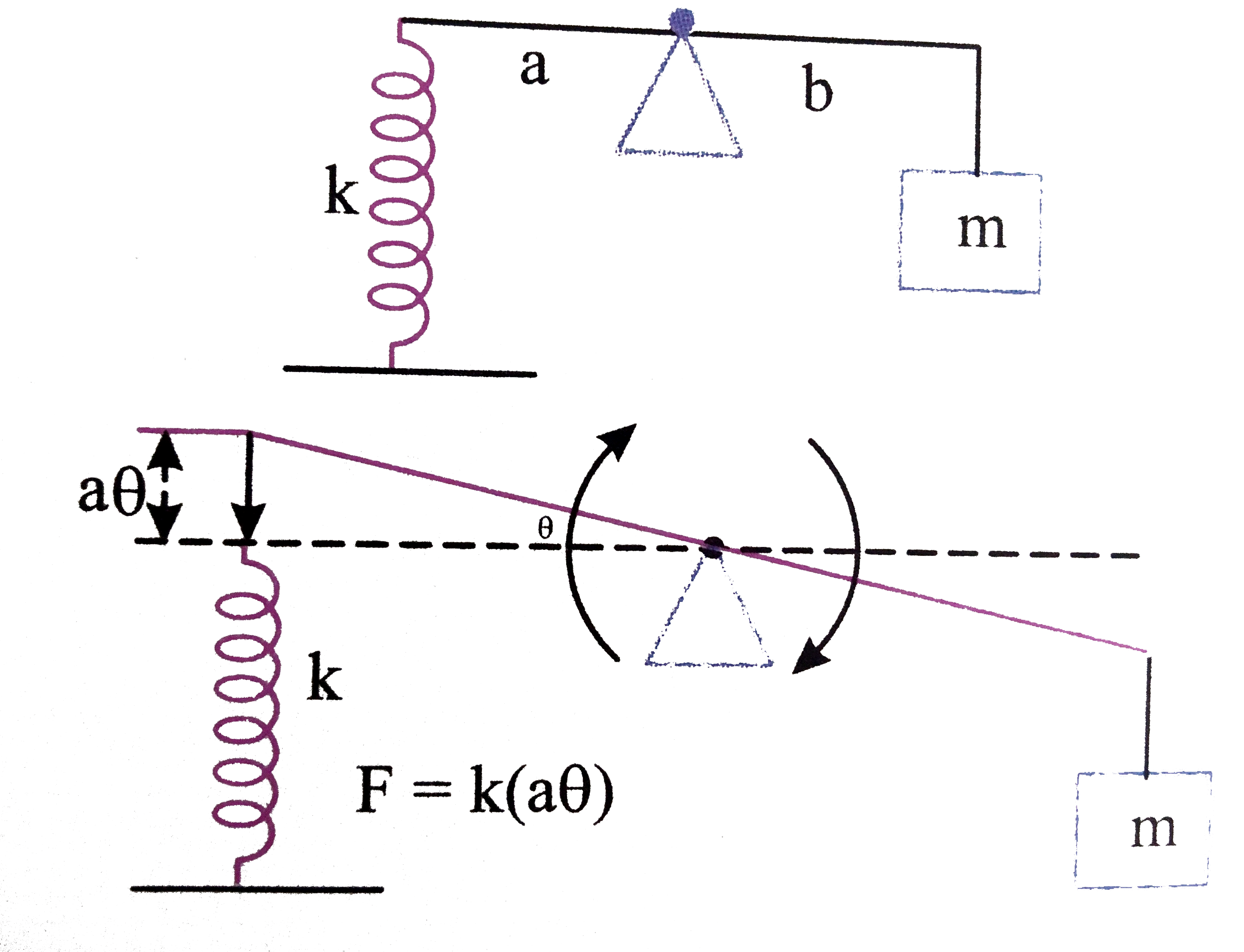
View SolutionA small block is connected to a mass less rod, which is turn is attached to a spring of force constant k as shown in Fig. The blcok is displaced down slightly, and left free. Find time period of small oscillations.
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA body of mass m = 2kg hangs from three springs, each of spring constant 1875 N/m, as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period
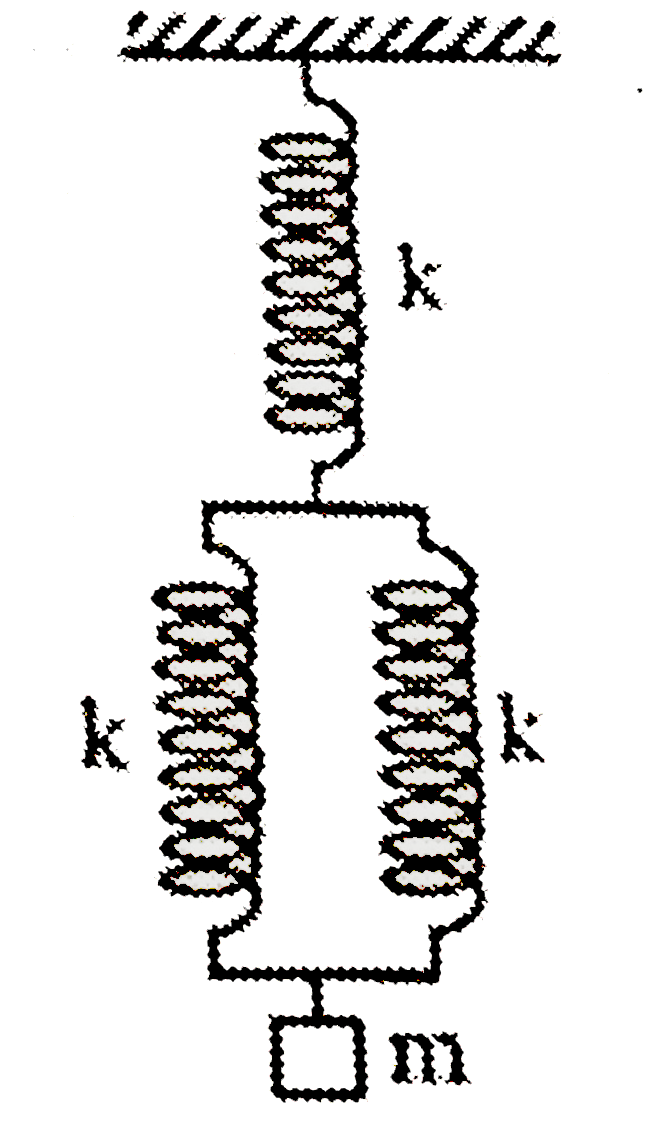
View Solution
