A point mass m=1kg is attached to a point P on the circumference of a uniform ring of mass M=3kg and radius R=2.0m. The ring is placed on a horizontal surface and is released from rest with line OP in horizontal position (O is centre of the ring). Friction is large enough to prevent sliding. Calculate the following quantities immediately after the ring is released-
(a) angular acceleration (α) of the ring,
(b) normal reaction of the horizontal surface on the ring and
(c) the friction force applied by the surface on the ring.
[Take g=10m/s2 ]
![A point mass m = 1 kg is attached to a point P on the circumference of a uniform ring of mass M = 3kg and radius R = 2.0 m. The ring is placed on a horizontal surface and is released from rest with line OP in horizontal position (O is centre of the ring). Friction is large enough to prevent sliding. Calculate the following quantities immediately after the ring is released- (a) angular acceleration (alpha) of the ring, (b) normal reaction of the horizontal surface on the ring and (c) the friction force applied by the surface on the ring. [Take g = 10 m//s^(2) ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C06_E01_101_Q01.png)
The correct Answer is:(a) 58rad/s2
(b) 1554N
(c) 5N
Step by step video, text & image solution for A point mass m = 1 kg is attached to a point P on the circumference of a uniform ring of mass M = 3kg and radius R = 2.0 m. The ring is placed on a horizontal surface and is released from rest with line OP in horizontal position (O is centre of the ring). Friction is large enough to prevent sliding. Calculate the following quantities immediately after the ring is released- (a) angular acceleration (alpha) of the ring, (b) normal reaction of the horizontal surface on the ring and (c) the friction force applied by the surface on the ring. [Take g = 10 m//s^(2) ] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Let →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

View SolutionA ring of mass m and radius r has a particle of mass m attached to it at a point A. the ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring is released from rest when AB is horizontal. find the angular veloicity and the angular acceleration of the body when AB has turned through an angle (pi)/(3) .
View SolutionA uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.

View SolutionFind the centre of mass of a uniform semicircular ring of radius R and mass M.
View SolutionA ring has a total mass M but non-uniformly distributed over its circumference. The radius of the ring is R . A point mass m is placed at the centre of the ring. Workdone in taking away this point mass from ecntre to infinity is
View SolutionA particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m and radius 'r' . The system is released from rest and rolls without sliding. The angular release is acceleration of ring just after release after

View Solution
A ring of mass M and radius R is held at rest on a rough horizontal surface. A rod of mass M and length L=2√3R is pivoted at its end A on the horizontal surface and is supported by the ring. There is no friction between the ring and the rod. The ring is released from this position. Find the acceleration of the ring immediately after the release if θ=60∘. Assume that friction between the ring on the horizontal surface is large enough to prevent slipping of the ring.
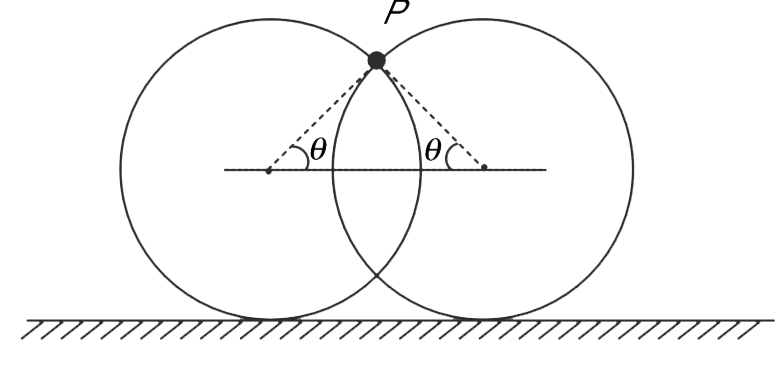
View SolutionTwo identical rings, each of mass M and radius R, are standing on a rough horizontal surface. The rings overlap such that the horizontal line passing through their centre makes an angle of θ=45∘ with the radius through their intersection point P. A small object of mass m is placed symmetrically on the rings at point P and released. Calculate the acceleration of the centre of the ring immediately after the release. There is no friction between the small object and the rings. The friction between the small object and the rings, and the friction between the rings and the ground is large enough to prevent slipping.
View SolutionA circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionFind potential at a point 'P' at a distance 'x' on the axis away from centre of a uniform ring of mass M and radius R .
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface. Friction is sufficient to prevent slipping. Find the frictional force acting on the ring.
View SolutionA force F is applied on the top of a ring of mass M and radius R placed on a rough horizontal surface. Friction is sufficient to prevent slipping. Find the frictional force acting on the ring.
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v_0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:
View Solution
