A potential energy function for a two-dimensional force is the form . Find the force that acts at the point .
To find the force that acts at the point (x,y) given the potential energy function U=3x2y−7x, we will use the relationship between force and potential energy in two dimensions. The force components can be derived from the potential energy function by taking partial derivatives.
1. Understand the relationship between force and potential energy:
The force F in two dimensions can be expressed as:
F=−∇U
where ∇U is the gradient of the potential energy function U.
2. Calculate the partial derivative with respect to x:
We need to find the force component in the x-direction, Fx, which is given by:
Fx=−∂U∂x
First, we calculate ∂U∂x:
U=3x2y−7x
Taking the partial derivative:
∂U∂x=∂∂x(3x2y)−∂∂x(7x)=6xy−7
Therefore, the force in the x-direction is:
Fx=−(6xy−7)=−6xy+7
3. Calculate the partial derivative with respect to y:
Next, we find the force component in the y-direction, Fy, which is given by:
Fy=−∂U∂y
Now, we calculate ∂U∂y:
∂U∂y=∂∂y(3x2y)−∂∂y(7x)=3x2−0=3x2
Therefore, the force in the y-direction is:
Fy=−3x2
4. Combine the force components:
The total force vector F acting at the point (x,y) is:
F=(Fx,Fy)=(−6xy+7,−3x2)
Final Answer:
The force that acts at the point (x,y) is:
F=(−6xy+7,−3x2)
The force F in two dimensions can be expressed as:
F=−∇U
where ∇U is the gradient of the potential energy function U.
We need to find the force component in the x-direction, Fx, which is given by:
Fx=−∂U∂x
First, we calculate ∂U∂x:
U=3x2y−7x
Taking the partial derivative:
∂U∂x=∂∂x(3x2y)−∂∂x(7x)=6xy−7
Therefore, the force in the x-direction is:
Fx=−(6xy−7)=−6xy+7
Next, we find the force component in the y-direction, Fy, which is given by:
Fy=−∂U∂y
Now, we calculate ∂U∂y:
∂U∂y=∂∂y(3x2y)−∂∂y(7x)=3x2−0=3x2
Therefore, the force in the y-direction is:
Fy=−3x2
The total force vector F acting at the point (x,y) is:
F=(Fx,Fy)=(−6xy+7,−3x2)
The force that acts at the point (x,y) is:
F=(−6xy+7,−3x2)
Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.3
Explore 26 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.4
Explore 16 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Exercise 8.1
Explore 25 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
View SolutionThe potential energy function of a particle due to some gravitational field is given by U=6x+4y. The mass of the particle is 1kg and no other force is acting on the particle. The particle was initially at rest at a point (6,8). Then the time (in sec). after which this particle is going to cross the 'x' axis would be:
View SolutionThe potential energy of configuration changes in x and y directions as U=kxy, where k is a positive constant. Find the force acting on the particle of the system as the function of x and y.
View SolutionThe potential energy for a force filed →F is given by U(x,y)=cos(x+y). The force acting on a particle at position given by coordinates (0,π/4) is
View SolutionA single conservative force acting on a particle varies as →F=(−Ax+Bx2)ˆiN, where A and B are constants and x is in meters. (a) Calculate the potential energy function U(x) associated with this force, taking U=0 at x=0. (b) Find the change in potential energy and the change in kinetic energy of the system as the particles moves from x=2.00m to x=3.00m.
View SolutionThe potential energy (in joules ) function of a particle in a region of space is given as:
U=(2x2+3y2+2x)
Here x,y and z are in metres. Find the maginitude of x compenent of force ( in newton) acting on the particle at point P ( 1m, 2m, 3m).
View SolutionThe potential energy of a force filed →F is given by U(x,y)=sin(x+y). The force acting on the particle of mass m at (0,π4) is
View SolutionThe potential energy function for the force between two atoms in a diatomic molecule is approximately given by U(x)=ax12−bx6 where a and b are constant and x is the distance between the atoms. Find the dissoociation energy of the molecule which is given as D=[U(x−∞)−Uatequilibrium]
View SolutionFigure shows a plot of potential energy function U(x)=kx2 where x=displacement and k=constant. Identify the correct conservative force function F(x)
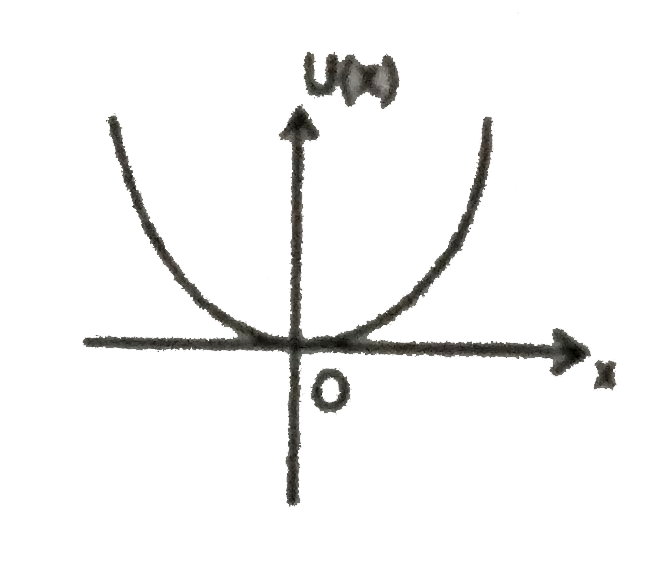
View SolutionThe potential energy function for the force between two in a diatomic molecule can approximately be expressed as U(x)=ax12−bx4, where a and b are positive constants, and x is the distance between the atoms. Answer the following question by selecting most appropriate alternative.
The graph between potential energy vs x will be
View Solution
