A rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
E=λ4πε0a(−ˆi)
E=λ4πε0a(ˆi)
E=λ2πε0a(−ˆi)
E=λ2πε0a(ˆi)
The correct Answer is:C
To find the electric field at the point x=−a due to a uniformly charged rod extending from the origin to infinity along the x-axis, we can follow these steps:
1. Understand the Setup:
- We have a rod lying along the x-axis from x=0 to x=∞ with a uniform charge density λ (in C/m).
- We want to find the electric field at the point P located at x=−a.
2. Consider an Element of Charge:
- Take a small element of the rod dx at a position x (where x is from 0 to ∞).
- The charge dq on this small element is given by:
dq=λdx
3. Calculate the Electric Field Contribution:
- The electric field dE at point P due to the charge dq is given by Coulomb's law:
dE=kdqr2
- Here, r is the distance from the charge element to point P. Since point P is at x=−a, the distance r can be expressed as:
r=x+a
- Therefore, the electric field contribution becomes:
dE=kλdx(x+a)2
4. Determine the Direction of the Electric Field:
- Since the rod has a positive charge, the electric field at point P will point towards the left (negative x-direction).
5. Integrate to Find the Total Electric Field:
- The total electric field E at point P is obtained by integrating dE from x=0 to x=∞:
E=∫∞0dE=∫∞0kλdx(x+a)2
6. Perform the Integration:
- The integral can be solved as follows:
E=kλ∫∞0dx(x+a)2
- The integral ∫dx(x+a)2 evaluates to −1x+a, so we compute:
E=kλ(−1x+a)∞0=kλ(0−(−1a))=kλa
7. Final Result:
- The total electric field at point P is:
E=kλa
- Since the direction is towards the left, we can express it as:
E=−kλa^i
- We have a rod lying along the x-axis from x=0 to x=∞ with a uniform charge density λ (in C/m).
- We want to find the electric field at the point P located at x=−a.
- Take a small element of the rod dx at a position x (where x is from 0 to ∞).
- The charge dq on this small element is given by:
dq=λdx
- The electric field dE at point P due to the charge dq is given by Coulomb's law:
dE=kdqr2
- Here, r is the distance from the charge element to point P. Since point P is at x=−a, the distance r can be expressed as:
r=x+a
- Therefore, the electric field contribution becomes:
dE=kλdx(x+a)2
- Since the rod has a positive charge, the electric field at point P will point towards the left (negative x-direction).
- The total electric field E at point P is obtained by integrating dE from x=0 to x=∞:
E=∫∞0dE=∫∞0kλdx(x+a)2
- The integral can be solved as follows:
E=kλ∫∞0dx(x+a)2
- The integral ∫dx(x+a)2 evaluates to −1x+a, so we compute:
E=kλ(−1x+a)∞0=kλ(0−(−1a))=kλa
- The total electric field at point P is:
E=kλa
- Since the direction is towards the left, we can express it as:
E=−kλa^i
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
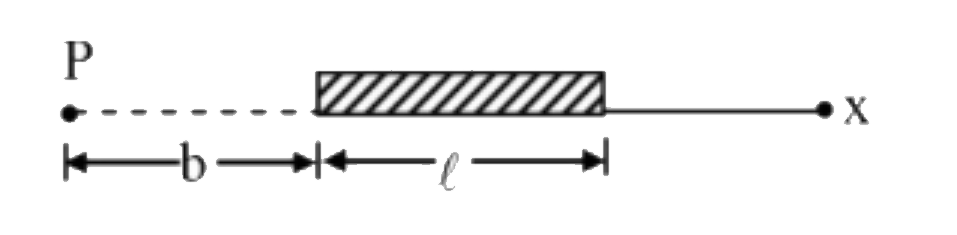
View SolutionA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?

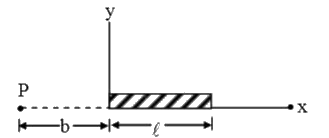
View SolutionA rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View SolutionA continuous line of charge of length 3d lies along the x-axis, extending from x + d to x + 4d, The line carries a uniform linear charge density lambd . In terms of d,λ and any necessary physical constant find the magnitude of the electric field at the origin.
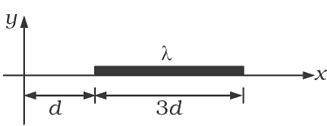
View SolutionAn electric dipole is placed at the origin along x-axis.The electric field at any point , whose position vector , makes an angle θ with the x-axis ,makes an angle,
View SolutionA uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
View SolutionA charged particle P leaves the origin with speed v=v0 at some inclination with the x-axis. There is a uniform magnetic field B along the x-axis. P strikes a fixed target T on the x-axis for a minimum value of B=B0. P will also strike T if
View Solution
